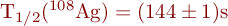radioaktiver

Einleitung
1 Aufgaben
2 Physikalische Grundlagen
3 Versuchsdurchführung

Einleitung

Radioaktive Stoffe und Präparate finden zunehmend Anwendung in vielen Bereichen von Wissenschaft und Technik. In der Medizin werden radioaktive Stoffe zur Diagnose und Therapie eingesetzt. Stoffwechselvorgänge und Funktionsabläufe können untersucht werden, indem man radioaktive Stoffe in ein Organ einbringt und deren örtliche und zeitliche Verteilung durch Messung der Strahlung sichtbar macht. In der Biologie und Chemie werden Transportvorgänge und Reaktionsverläufe durch Markierung mit radioaktiven Substanzen untersucht. Durch Bestrahlung können einfach und gezielt genetische Mutationen erzeugt werden. Altertums-, Erd- und Biowissenschaften machen Gebrauch von der ¹⁴C-Methode zur Altersbestimmung. In der Technik werden radioaktive Präparate für Überwachungs- und Regelzwecke und zur zerstörungsfreien Werkstoffprüfung eingesetzt.

Von radioaktiver Strahlung können erhebliche Gefahren für den Menschen ausgehen. Der Umgang mit radioaktiver Strahlung und radioaktiven Materialien ist daher gesetzlich geregelt, und die Vorschriften des Strahlenschutzes müssen genau beachtet werden!

Die Aktivität des in den Versuchen benutzten Neutronengenerators ist vergleichsweise gering. Seine Dosisleistung liegt in 1 m Abstand in der Größenordnung der natürlichen Strahlung, und eine zählende Belastung und ein zusätzliches Risiko sind bei der kurzfristigen Arbeit an den Versuchsplätzen nicht gegeben. Dennoch sind zur Arbeit an den Versuchsplätzen die grundsätzlichen Regeln der Strahlenschutzanweisung im allgemeinen Teil des Skripts zu beachten.

Ein wichtiges Ziel der Versuche Radioaktiver Zerfall und Gamma-Spektroskopie ist es, durch Vermittlung der Grundlagen der quantitativen Erfassung und Bewertung von Strahlenwirkungen (Dosimetrie) eine kritische Beurteilung von Strahlenwirkungen möglich zu machen.

1 Aufgaben

(Dosisleistungsmessung) Zur sofortigen Auswertung: Messung der natürlichen $\gamma$ -Ionendosisleistung direkt an der Außenwand des für den Versuch vorhandenen Neutronengenerators und in größerem Abstand (ca. 3m). Umrechnung auf die Äquivalentdosisleistung (in mSv pro Jahr).
(Zerfallsgesetz): Messung der Zerfallskonstanten der Radionuklide ¹⁰⁸Ag und ¹¹⁰Ag. Angabe der Halbwertszeiten und mittleren Lebensdauern.
(Anfangsaktivitäten): Angabe und Vergleich der Anfangsaktivitäten der beiden Silber-Isotope für die verschiedenen Aktivierungszeiten.

2 Physikalische Grundlagen

2.1 Radioaktiver Zerfall

Atomkerne sind aus Protonen und Neutronen aufgebaut. Die Zahl der Protonen (P) ist gleich der Anzahl der Elektronen in der Hülle des Atoms; sie bestimmt das Element und die chemischen Eigenschaften. Die Zahl der Neutronen (N) ist bei leichten Kernen etwa gleich, bei schweren Kernen größer als die Protonenzahl. Die Summe aus P und N heißt Nukleonenzahl A. Von allen Elementen existieren Modifikationen mit unterschiedlicher Neutronenzahl, die Isotope genannt werden. Die Kennzeichnung eines speziellen Isotops geschieht durch Angabe des Buchstabensymbols für das Element und die Massenzahl. Aus diesen Angaben gehen auch die Protonenzahl P und die Neutronenzahl N hervor, z.B.:

$\mathrm{(1)}\ \ \ ^{\mathrm{Nukleonenzahl}}_{\mathrm{Ladungszahl}} \ \mathrm{Element}_{\mathrm{\ Neutronenzahl}} = ^{137}_{55}\mathrm{Cs}_{82} = ^{137}\mathrm{Cs}.$

Isotope mit vom obigen "Gleichgewichtszustand" abweichender Neutronenzahl sind energetisch instabil und wandeln sich spontan unter Aussendung von Teilchen um (Radionuklide; radioaktiver Zerfall). Die Umwandlungen erfolgen durch -Zerfall oder -Zerfall (; ; EC = electron capture), wobei sich die Protonenzahlen und damit die chemische Natur der Atome ändern. Nach dem Zerfall befinden sich die Folgekerne im Allgemeinen in einem angeregten Zustand höherer Energie, aus dem sie unter Aussendung von elektromagnetischer Strahlung (-Strahlung) in den Grundzustand übergehen.

-Zerfall: Bei schweren Kernen wird ein ganzes Bruchstück aus zwei Protonen und zwei Neutronen (He-Kern, -Teilchen) abgespalten, wodurch sich das Verhältnis von Neutronenzahl zu Protonenzahl verändert, z.B.:

$\mathrm{(2)} \ \ \ ^{236}_{92}\mathrm{U}_{144} \overset{\alpha}{\longrightarrow} \ ^{232}_{90}\mathrm{Th}^*_{142} + ^{4}_{2}\mathrm{He}_{2}$

Der * beim Folgekern ²³²Th kennzeichnet, dass sich der Kern in einem angeregten Zustand befindet.

-Zerfall: Beim -Zerfall wandelt sich ein Neutron in ein Proton um oder umgekehrt. Dabei werden Elektronen (-Strahlung) oder Positronen (-Strahlung) und zusätzlich sogenannte Antineutrinos () oder Neutrinos ( $\bar \nu$ ) emittiert:

$\mathrm{(3)} \ \ \ \mathrm{n} \longrightarrow \mathrm{p} + \mathrm{e}^- +\bar \nu \ \ \mathrm{oder}$ $\mathrm{p} \longrightarrow \mathrm{n}+ \mathrm{e}^+ +\nu.$

EC (Elektroneneinfang; electron capture): Der Elektroneneinfang entspricht einem -Zerfall in umgekehrter Richtung, wobei ein Kernproton ein Hüllenelektron einfängt (s-Elektronen haben eine zwar kleine, aber nicht verschwindende Aufenthaltswahrscheinlichkeit am Ort des Kerns):

$\mathrm{(4)} \ \ \ \mathrm{p}+\mathrm{e}^- \longrightarrow \mathrm{n} + \nu.$

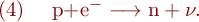
-Strahlung: Nach radioaktiven Umwandlungen befinden sich die Folgekerne häufig in energetisch angeregten Zuständen (*; s.o.). Sie gehen mit unterschiedlichen Übergangswahrscheinlichkeiten (bzw. mittleren Lebensdauern oder Halbwertszeiten als äquivalenten Parametern) weiter in den Grundzustand über, wobei die freiwerdende Energie in Form von (elektromagnetischer) -Strahlung ausgesandt wird, z.B.:

$\mathrm{(5)} \ \ \ ^{137}\mathrm{Ba}^* \overset{\gamma}{\longrightarrow} \ ^{137}\mathrm{Ba} + \gamma.$

2.2 Dosimetrie

Die Dosimetrie erfasst quantitativ die physikalischen und biologisch-physiologischen Wirkungen von Strahlung auf organische Materie; sie ist ein für Medizin und Biologie wichtiges Arbeitsgebiet. Bei den Betrachtungen muss zwischen Ursache und Wirkung unterschieden werden. Ursachen von Strahlenbelastungen sind radioaktive Quellen, deren Stärke durch ihre Aktivität, d.h. die Anzahl der Zerfälle pro Zeit in der Maßeinheit 1 Bq (Bequerel) = 1 Zerfall pro Sekunde gemessen wird.

Die Wirkungen beziehen sich immer auf eine Probe im Strahlungsfeld, die eine bestimmte Strahlungsmenge pro Masse, die Dosis, durch Absorption aufnimmt: gibt es nichts oder Niemanden in der Nähe eines Strahlers, so gibt es auch keine Folgen. Die physikalisch-makroskopischen Folgen sind zunächst ein im Probekörper deponierter Betrag an Energie. Die primären mikroskopisch-chemischen Folgen sind Ionisationen oder andere komplizierte Veränderungen der chemisch-atomaren oder molekularen Struktur der Probensubstanz, die dann Ursache für nachfolgende physiologische und biologische Strahlenschädigungen sind.

Bringt man eine Probe (z.B. Muskel- oder Weichteilgewebe als organischen Körper) in ein radioaktives Strahlungsfeld, so wird ein Teil der Strahlungsenergie absorbiert, während ein anderer Teil die Probe oder den Körper ohne Wechselwirkung, und damit ohne Schädigung, durchläuft.

Als Maß für die aufgenommene (absorbierte) Strahlung wird zunächst die Energiedosis als absorbierte Energie pro Masse definiert. Dosisangaben beziehen sich immer auf eine bestimmte Probe und einen bestimmten Stoff als Probensubstanz. Sie charakterisieren aber auch die Stärke eines Strahlungsfeldes durch die Betrachtung, dass diese Energie aufgenommen würde, wenn sich die entsprechende Probe am Ort dieses Strahlungsfeldes befände:

$\mathrm{(6)} \ \ \ D_E = \frac{\mathrm{absorbierte \ Strahlungsenergie}}{\mathrm{Masse}}= \frac{\Delta E}{m}.$

Die Einheit der Energiedosis ist:

$\mathrm{(7)} \ \ \ [D_E] = 1 \frac{\mathrm{J}}{\mathrm{kg}} = 1 \mathrm{Gy} \ \ \mathrm{(Gray)}.$

Die Energiedosis ist schwer direkt messbar, da die bei praktischen Betrachtungen gegebenen Energiemengen sehr gering sind (eine für den Menschen 100-%-ig letale Strahlendosis beträgt etwa 8 J/kg. Vergleiche: Zur Temperaturerhöhung von Wasser um 1 K sind 4200 J/kg erforderlich, d.h. die Energie einer tödlichen Strahlendosis entspricht der Wärmemenge eines Schluckes Kaffee! Physikalisch und messtechnisch gut nachweisbar ist das Ionisationsvermögen radioaktiver Strahlung und als praktische Messgröße wird daher zusätzlich die Ionendosis mit Luft als Probensubstanz definiert:

$\mathrm{(8)} \ \ \ D_Q = \frac{\Delta Q}{m_{\mathrm{Luft}}. <\latex} Die Einheit ist: <latex> \mathrm{(9)} \ \ \ [D_Q] = 1 \frac{\mathrm{C}}{\mathrm{kg_{Luft}}} = 1 \frac{\mathrm{As}}{\mathrm{kg_{Luft}}}.$

Die Ionendosis kann direkt mit sogenannten Ionisationskammern gemessen werden.

Der Zusammenhang zwischen Energie- und Ionendosis hängt einerseits vom Probenmaterial und andererseits von der Quantenenergie der Strahlung ab. Für Muskel- und Weichteilgewebe gilt in guter Näherung in weiten Bereichen unabhängig von der Quantenenergie:

$\mathrm{(10)} \ \ \ D_E \approx 40 \frac{\mathrm{Gy}}{\mathrm{C/kg}} D_Q.$

Die biologische Strahlenwirkung wird darüber hinaus auch von der Strahlenart bestimmt, was in einem zusätzlichen Faktor für die relative biologische Wirksamkeit (RBW-Faktor) zum Ausdruck gebracht wird (Tab. 1):

Strahlenart	RBW-Faktor
-,-Strahlung	1
langsame Neutronen	5
-Strahlung, schnelle Neutronen	10
Röntgenstrahlung	5…10

Tab.1 RBW-Faktoren

Die Energiedosis multipliziert mit dem RBW-Faktor ergibt dann die wirkungsrelevante Äquivalentdosis = RBW $\cdot D_E$ .

Die Einheit der Äquivalentdosis ist, genau wie die der Energiedosis, 1 J/kg; sie wird zur Unterscheidung jedoch 1 Sv (Sievert) genannt:

$\mathrm{(11)} \ \ \ [D_{Ä}] = 1 \frac{\mathrm{J}}{\mathrm{kg}} = 1 \mathrm{Sv} \ \ \mathrm{(Sievert)}.$

Neben den Dosiswerten tritt insbesondere als praktische Messgröße vielfach die auf die Zeit bezogene Dosis, d.h. die Dosisleistung auf.

2.3 Zeitgesetze des radioaktiven Zerfalls

Der radioaktive Zerfall ist ein zufälliger (stochastischer) Prozess, für den über den Zeitpunkt des Zerfalls keine deterministisch bestimmten, sondern nur Wahrscheinlichkeits- bzw. statistische Erwartungsvorhersagen für ein Ensemble von Kernen gemacht werden können. Für einen betrachteten radioaktiven Kern wird die Wahrscheinlichkeit zu zerfallen als proportional zur Beobachtungsdauer dt angenommen, so dass für die Anzahl der Zerfälle dN einer Probe von N Kernen gilt:

$\mathrm{(12)} \ \ \ \mathrm{d}N = - \lambda N \mathrm{d}t \ \mathrm{bzw.} \ \frac{\mathrm{d}N}{\mathrm{d}t} = - \lamda N(t).$

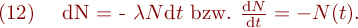
Das negative Vorzeichen berücksichtigt die Abnahme von N mit der Zeit. Als Lösung der Differentialgleichung (12) wird eine Funktion N(t) gesucht, deren Ableitung (bis auf einen Faktor) gleich der Funktion selbst ist. Diese Bedingung erfüllt die e-Funktion, und man erhält als radioaktives Zerfallsgesetz:

$\mathrm{(13)} \ \ \ N = N_0 \mathrm{e}^{- \lambda t}.$

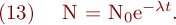
Der Proportionalitätsfaktor $\lambda$ im Exponenten heißt Zerfallskonstante. Sie kennzeichnet die Wahrscheinlichkeit des radioaktiven Zerfalls und ist für die einzelnen Radionuklide charakteristisch. Äquivalente Größen sind die mittlere Lebensdauer oder die Halbwertszeit $T_{1/2}$ . Die Zusammenhänge zwischen den Größen sind:

$\mathrm{(14)} \ \ \ \tau = \frac{1}{\lambda} \ \ \mathrm{bzw.} \ \ T_{1/2}= \tau \mathrm{ln}2= \frac{\mathrm{ln}2}{\lambda}.$

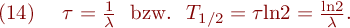
Nach der Zeitdauer $T_{1/2}$ ist die Zahl radioaktiver Kerne einer Probe auf die Hälfte, nach der Zeitdauer $\tau$ auf den e-ten Teil (1/e $\approx$ 1/2,72 $\approx$ 0,37 = 37 %) zurückgegangen.

Als Aktivität A wird die Zahl der Zerfällt pro Zeit - dN/dt bezeichnet. Man erhält:

$\mathrm{(15)} \ \ \ A(t) = -\frac{\mathrm{d}N}{\mathrm{d}t} = \lambda N(t) = A_0 \mathrm{e}^{-\lambda t} \ \mathrm{mit} \ A_0 = \lambda N_0$

Die Einheit der Aktivität ist 1 s ^-1 (pro Sekunde) gleich 1 Bq (Bequerel).

2.4 Kernreaktionen

Neben dem spontanen Zerfall können Kernumwandlungen auch durch äußere Einflüsse verursacht werden, z.B. durch Kernreaktionen. Trifft ein freies Neutron auf einen Atomkern, so kann es eingefangen werden. Der Atomkern wird zu einem radioaktiven, sogenannten Zwischenkern, der anschließend weiter zerfällt.

Bestimmte Uranisotope zerfallen nach Neutroneneinfang in zwei etwa gleich große Bruchstücke (Kernspaltung). Dabei werden wieder Neutronen freigesetzt, die weitere Kernreaktionen auslösen können (Kettenreaktionen).

2.5 Radioaktives Gleichgewicht und Sättigungsaktivität

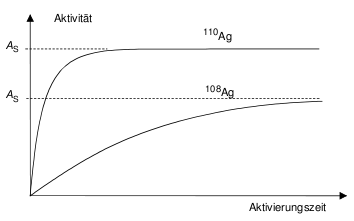
Bei der Herstellung radioaktiver Kerne oder angeregter Zustände (z.B. durch Kernreaktionen) stehen der Aktivierungsprozess und der gleichzeitig einsetzende radioaktive Zerfall in Konkurrenz zueinander. Zunächst wächst die Anzahl der radioaktiven Kerne, wobei aber auch die Zahl der Zerfälle zunimmt. Im Endzustand stellt sich ein radioaktives Gleichgewicht mit einer dann konstanten Aktivität ein (Sättigungsaktivität), bei dem die Anregungsrate und die Zerfallsrate gleich groß sind. Dieser Sättigungszustand wird dabei um so eher erreicht, je schneller der Zerfall erfolgt, d.h. je kleiner die Halbwertszeit des jeweiligen Zerfalls ist (siehe Abb. 1).

Ist nach einem radioaktiven Zerfall der Folgekern wiederum radioaktiv, so ergeben sich radioaktive Zerfallsketten oder Mutter-Tochter-Systeme. Derartige Mutter-Tocher-Systeme haben große Bedeutung in der medizinischen Anwendung zur Gewinnung kurzlebiger Radionuklide (Generatorsystem).

!! Abb. 1: !! ¹¹⁰Ag erreicht (bei gleicher Isotopenhäufigkeit in der Probe) eine größere Sättigungsaktivität wegen des größeren Wirkungsquerschnitts bei der Aktivierung und einen schnelleren Anstieg zum Gleichgewicht wegen der kürzeren Halbwertszeit.

2.6 Nachweissysteme

Geräte zum Strahlungsnachweis nennt man Strahlungsdetektoren. Die meisten Detektoren nutzen das Ionisationsvermögen der radioaktiven Strahlung aus. In einem nicht- oder schlechtleitenden Material (Gase, Halbleiter) werden durch Ionisation freie Ladungsträger erzeugt, die in einem elektrischen Messkreis einen nachweisbaren Strom- oder Spannungsimpuls verursachen. Beispiele für derartige Detektoren sind Ionisationskammern, Proportionalzählrohre, Geiger-Müller-Zählrohre (Auslösezählrohre) und Halbleiterdetektoren. Bei diesem Versuch wird der Strahlungsnachweis mit einem Geiger-Müller-Zählrohr (GM-Zählrohr) durchgeführt, das sehr einfach in Aufbau und Betrieb ist. Geiger-Müller-Zählrohre besitzen jedoch kein Energieauflösungsvermögen (siehe Versuch GAMMA-SPEKTROSKOPIE), d.h. jedes Strahlungsquant löst unabhängig von seiner Quantenenergie ein einheitliches Signal aus. Sie sind wegen ihrer relativ großen Totzeit auf kleine Zählraten beschränkt.

2.7 Fehler von Zählgrößen beim radioaktiven Zerfall

Der radioaktive Zerfall verhält sich als spontaner Prozess zufällig und unterliegt statistischen Gesetzmäßigkeiten. Die Anzahl der Zerfälle in einem bestimmten Zeitintervall z.B. ist normalverteilt, wobei die Standardabweichung als Fehler des einzelnen Messwerts gleich der Wurzel aus der Anzahl der registrierten Ereignisse N ist:

$\mathrm{(16)} \ \ \ \mathrm{Messwert \ } N \mathrm{\ mit \ Fehler \ } \Delta N = \sqrt{N}.$

Beispiel: Werden in 10s 1327 Ereignisse registriert, so ist der Fehler $\sqrt{1327}=37$ , das Ergebnis also $N=(1327 \pm 37)$ Ereignisse (bzw. als Endergebnis korrekt gerundet: $N=(1,33 \pm 0,04) 10^3$ Ereignisse). Werden Ereignisse zusammengefasst (addiert) oder voneinander abgezogen (Subtraktion von Untergrund), so gilt die Wurzelregel in beiden Fällen für die Summe der Ereignisse; d.h.

$\Delta(1327+158) = \Delta(1327-158) = \Sqrt{1485} = 39.$

3 Versuchsdurchführung

Zu Aufgabe 1: Dosisleistungsmessung

Die praktisch wichtige Messgröße der Dosimetrie ist die Dosisleistung, d.h. die auf die Zeit bezogene Dosis. Am Versuchsplatz ist ein in pA/kg ( = 10^-12 C pro s und kg) kalibriertes Ionendosisleistungsmessgerät vorhanden. Wegen der vergleichsweise geringen Anzahl der Ereignisse zeigen die Messwerte eine ausgeprägte stochastische Charakteristik mit einer erheblichen Schwankungsbreite, so dass ein Schätzwertintervall für die Dosisleistung durch Beobachtung über eine angemessen lange Zeit ermittelt werden muss.

Zu Aufgabe 2 (Zerfallsgesetz): Apparatur, Nulleffekt, Messtabelle

Der Strahlungsnachweis geschieht mit einem Geiger-Müller-Zählrohr, das sich innerhalb einer zylindrischen Bleiabschirmung befindet. Zur Messung der Aktivität (Zählrate) in Abhängigkeit von der Zeit ist ein automatischer Zähler vorhanden, der periodisch alle 10 s eine Messung mit folgendem Funktionsablauf durchgeführt:

Rücksetzen der Zählers auf 0 (reset);
Ereigniszählung (ca. 9 s);
Stopp zur Ablesung (ca. 1 s).

Das Ablesen und Protokollieren der Daten im 10-s-Takt bei einer Gesamtmesszeit von 15 Minuten (s.u.) erfordert Konzentration. Um Fehler in der Zeitachse durch unterlassene Ablesungen zu vermeiden, ist daher eine Kette von fünf Leuchtdioden am Zählgerät vorhanden, die in der Folge der Messwerte nacheinander aufleuchten und nach dem Ablauf von jeweils fünf Messungen gemeinsam erlöschen. Legt man im Messprotokoll eine Tabelle mit Blocks von fünf Feldern an, so lässt sich der korrekte Ablauf der Messung kontrollieren. Machen Sie sich vor Beginn der Messungen mit der Apparatur vertraut.

Vor Beginn der Messungen ist der Nulleffekt (Untergrund U), d.h. die Zählrate ohne radioaktive Probe, zu bestimmen. Der Nulleffekt kann auch mit Hilfe des automatischen Zählzyklus, oder aber auch durch eine "unmittelbare" ununterbrochene Messung bestimmt werden, wobei dann der Wert auf das tatsächliche Zähl-Zeitintervall von 9 s umzurechnen ist. Der Untergrund ist später von den einzelnen Messwerten punktweise abzuziehen.

Für die spätere Auswertung werden neben den gemessenen Zeit (t)- und Ereignis-Messwerten $(N=N_{Mess}-U)$ , die aus der grafischen Darstellung für große Zeiten extrapolierten Werte für ¹⁰⁸Ag $(N_{108})$ und die Messwerte für ¹¹⁰Ag als Differenzen zu den Werten von ¹⁰⁸Ag benötigt $(N_{110}=N-N_{108})$ ; siehe dazu auch die nachfolgende Beschreibung der Auswertung. Zur übersichtlichen Dokumentation aller Daten empfiehlt es sich, eine Messtabelle so anzulegen, dass sie bereits Spalten für diese weiteren Werte berücksichtigt (siehe Tabelle 2):

	$N_{Mess}$	$N_{108 + 110}=N_{Mess}-U$	$N_{108}$ (extrapoliert)	$N_{110}=N_{108+110}-N_{108}$
5
15
25
35
45
…
…

Tabelle 2: Vorschlag für die Messtabelle

Zerfallsgesetz

Am Versuchsplatz ist ein Zylinder aus Silberblech vorhanden, der um das Zählrohr gebracht werden kann. Die Messungen werden nacheinander für zwei verschiedene Aktivierungszeiten (1 min und 12 min) durchgeführt, wofür die Silberzylinder zunächst in einem der Kanäle der Neutronenquelle aktiviert werden.

Zur späteren korrekten Bestimmung der Anfangsaktivitäten ist es sehr wichtig, bei Ende der Aktivierung gleichzeitig mit dem Herausnehmen der Probe aus dem Generator den Messzyklus am Zählgerät zu starten, unabhängig davon, wie schnell der Silberzylinder über das Zählrohr gebracht werden kann. (Der erste Messwert ist damit nicht korrekt und wird später vom funktionalen Verlauf abweichen, was für die Auswertung der Messung aber unerheblich ist.)

Die Messungen sind für beide Aktivierungszeiten über (wenigstens) 15min zu erstrecken, auch wenn gerade bei der kurzen Aktivierungszeit der Eindruck entsteht, dass die Zählrate schon nach kürzerer Zeit bis auf den Nulleffekt abgeklungen ist. Die Halbwertszeit des kurzlebigen Isotops ¹¹⁰Ag beträgt 24 s und die des langlebigeren Isotops ¹⁰⁸Ag 144 s. Für eine eindeutige Abgrenzung der beiden unterschiedlichen Komponenten und Festlegung des Kurvenverlaufs der Abklingkurve für das langlebige Isotop ist eine Beobachtung über mindestens fünf Halbwertszeiten erforderlich.

Auswertung

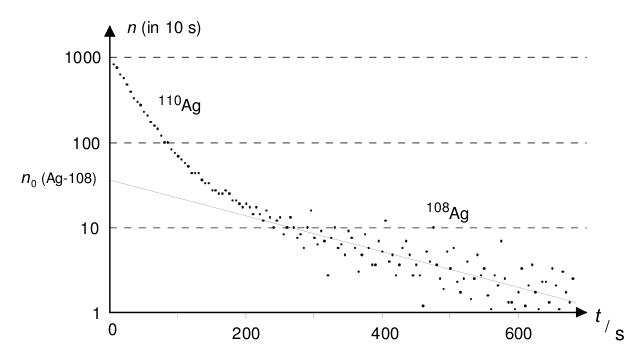
Zur Auswertung werden die um den Nulleffekt korrigierten Messwerte einfachlogarithmisch dargestellt. Als Zeitpunkte der 10-s-Zählintervalle werden den einzelnen Werten die Intervallmitten zugeordnet (für das erste 10-s-Intervall also s, usw.; siehe auch Beispiel der schematischen Darstellung der Messtabelle). Die Messung hat typischerweise den in Abb. 2 gezeigten Verlauf.

!! Abb. 2: !! Grafische Darstellung der Messergebnisse. Zählrate logarithmisch über der Zeit und Ausgleichsgerade für ¹⁰⁸Ag.

Zunächst wird durch den flacheren, rechten Teil der Kurve (ab etwa t=150 s) eine Ausgleichsgerade für ¹⁰⁸Ag gelegt, und aus der Steigung die Zerfallskonstante berechnet. Dabei ist es günstig, die Messwerte bis etwa 150 s abzudecken, um bei der Festlegung der Ausgleichsgeraden nicht durch den Beitrag der schnellen Komponente von ¹¹⁰Ag beeinflusst zu werden.

Danach werden von Messpunkten des steileren, linken Teils der Kurve punktweise die Anteile ¹⁰⁸Ag abgezogen, die man der extrapolierten Ausgleichsgeraden entnimmt. Die so erhaltenen Werte für ¹¹⁰Ag werden in einer zweiten Darstellung erneut einfachlogarithmisch und mit einem geeignet gestreckten Zeitmaßstab dargestellt und ausgewertet. Die Zerfallskonstanten werden aus den Steigungen der Geraden gemäß (15) und die Halbwertszeiten nach (14) berechnet.

Zu Aufgabe 3: Anfangsaktivitäten

Die Anfangszählraten für können an den Schnittpunkten mit der Ordinate abgelesen werden. Die Werte sind im Vergleich zu dem erwarteten Verhalten gemäß Abb. 1 qualitativ zu diskutieren.

Literaturwerte

Mittlere natürliche Äquivalentdosisleistung für die Bundesrepublik Deutschland:

= 1,3 mSv/a (Schwankungsbreite unbekannt)

Halbwertszeiten (KOHLRAUSCH; Praktische Physik 3; Teubner):

$T_{1/2}(^{108}\mathrm{Ag}) = (144 \pm 1) \mathrm{s}$

$T_{1/2}(^{110}\mathrm{Ag}) = (24,4 \pm 0,2) \mathrm{s}$

Table of Contents