Table of Contents
<texit info> author=laehnemann title=V5 </texit>
V5 - Versuchsanleitung
| V5 | THERMISCHE ISOLIERUNG |
|---|
Einführung
Warum tragen wir im Sommer und im Winter Kleidung aus unterschiedlichen Materialien und unterschiedlicher Dicke?
Warum hat die Kleidung der Astronauten als oberste Schicht eine dünne Aluminiumhaut?
Die diesen Fragen zugrunde liegenden Mechanismen des Wärmeaustauschs zwischen einem System und seiner Umgebung sollen an einem einfachen Beispiel untersucht werden.
Von einem Körper wird Wärmeenergie auf drei Arten an die (kältere) Umgebung abgegeben:
- durch Konvektion (Wärmetransport, der mit Materietransport verbunden ist);
- durch Wärmeleitung (in Materie, jedoch ohne Materietransport);
- durch Wärmestrahlung (elektromagnetische Strahlung).
Geben Sie Beispiele für diese verschiedenen Transportmechanismen an.
Bei den vier im Versuch verwendeten und mit Wasser gefüllten Gefäßen werden von Gefäß zu Gefäß die Möglichkeiten des Wärmeaustauschs ausgeschaltet (siehe Tabelle 1).
Tabelle 1: Arten des Wärmeaustauschs in unterschiedlichen Glasgefäßen: Gefäß 1 = einfaches Glasgefäß; Gefäß 2 = doppelwandiges Glasgefäß; Gefäß 3 = doppelwandiges Glasgefäß (evakuiert); Gefäß 4 = Dewargefäß (doppelwandig, evakuiert und verspiegelt).
| Wärmeaustausch durch | |||
|---|---|---|---|
| Konvektion | Wärmeleitung | Wärmestrahlung | |
| Gefäß 1 | ja | ja | ja |
| Gefäß 2 | nein | ja | ja |
| Gefäß 3 | nein | nein | ja |
| Gefäß 4 | nein | nein | nein |
Bei allen Gefäßen wird zusätzlich Wärme über die Wasseroberfläche abgegeben. Die Gefäße sollten daher die gleiche Querschnittsfläche haben, damit dieser Störeffekt in allen Fällen gleich groß ist1).
Das Ziel des Versuchs ist es, aus den verschiedenen Geschwindigkeiten, mit denen sich das Wasser in den Gefäßen abkühlt, abzuschätzen, wie viel die einzelnen Mechanismen (Konvektion, Wärmeleitung und Wärmestrahlung) zum Temperaturausgleich beitragen.
Grundlagen
Da die Abkühlgeschwindigkeit eines Körpers nur von der Temperaturdifferenz zu seiner Umgebung abhängt, ist es zweckmäßig, mit der zeitabhängigen Differenz zwischen Wassertemperatur <latex>T(t)</latex> und Umgebungstemperatur <latex>T_U</latex>, der so genannten Übertemperatur <latex>\theta(t) = T(t) - T_{U}</latex>, zu rechnen.
Ein Körper kühlt umso schneller ab, je größer die Temperaturdifferenz zur Umgebung ist:
<latex> $\begin{align*} -\frac{d\theta}{dt} \sim \theta . \end{align*}$ </latex> (1)
Diese Proportionalität lässt sich mathematisch durch die Gleichung
<latex> $\begin{align*} \frac{d\theta}{dt} = - a \cdot \theta \end{align*}$ </latex> (2)
beschreiben.
Das Minuszeichen besagt bei positiv eingeführter Konstante <latex> a </latex>, dass es sich mit fortschreitender Zeit um eine Abnahme der Temperatur handelt (<latex>dt > 0</latex> und <latex>d\theta < 0</latex>). Gleichung (2) wird durch die Exponentialfunktion erfüllt:
<latex> $\begin{align*} \theta(t) = \theta(0) \cdot e^{-a \cdot t} , \end{align*}$ </latex> (3)
mit <latex>\theta(0) = \theta(t=0)</latex>. Trägt man für die vier Gefäße die gemessenen Übertemperaturen als Funktion der Zeit <latex>t</latex> auf, sollten sich fallende Exponentialfunktionen ergeben, die umso flacher verlaufen, je besser die Isolierung des jeweiligen Gefäßes ist (siehe Abbildung 1A).
Ein Maß für die Wirksamkeit der Isolierung ist die Konstante <latex> a </latex> in der Exponentialfunktion in (3); sie gibt an, wie schnell die Temperatur mit der Zeit abfällt. Diese Konstante <latex> a </latex> heißt deshalb Abkühlrate; ihre Einheit ist <latex>[a] = \mathrm{min}^{-1}</latex>.
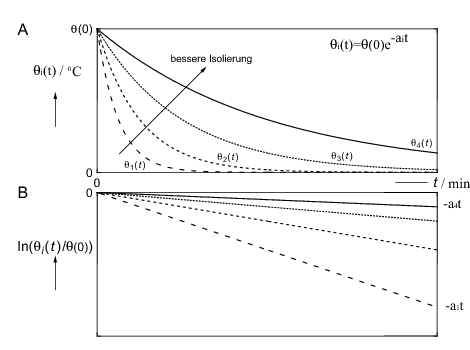
Abbildung 1: (A) Graphische Darstellung der Exponentialfunktion <latex>\theta_{i}(t) = \theta(0) \cdot e^{-a_{i} \cdot t}</latex> für vier verschiedene Werte <latex>a_{1} > a_{2} > a_{3} > a_{4}</latex>. (B) Auftragung der Funktionen <latex>\lnlatex_begin_align_frac_theta_t_theta_0_e_-a_cdot_t_end_align_latex_4_latex_begin_align_ln_left_frac_theta_t_theta_0_right_-_a_cdot_t_._end_align_latex_5_als_steigung_der_geraden_erhaelt_man_die_negativen_abkuehlraten_latex_-a_1_ldots_-a_4_latex_der_vier_verschiedenen_gefaesse_die_steigungsdreiecke_zur_bestimmung_der_geradensteigung_sollten_moeglichst_gross_sein_damit_die_fehler_von_latex_a_1_ldots_a_4_latex_klein_bleiben_vgl._uebung_ue2_._die_waermeenergie_latex_q_latex_die_ein_koerper_der_masse_latex_m_latex_und_der_spezifischen_waermekapazitaet_latex_c_latex_abgibt_wenn_er_sich_um_eine_temperaturdifferenz_latex_theta_latex_abkuehlt_ist_latex_begin_align_q_c_cdot_m_cdot_theta_._end_align_latex_6_da_sich_in_diesem_versuch_die_uebertemperatur_latex_theta_t_latex_mit_der_zeit_aendert_kleiner_wird_aendert_sich_auch_die_abgegebene_waermeenergie_latex_q_t_latex_._die_aenderung_latex_dq_dt_latex_bezeichnet_man_als_waermestrom_oder_waermestromstaerke._es_gilt_also_latex_begin_align_frac_dq_dt_c_cdot_m_cdot_frac_d_theta_dt_._end_align_latex_7_mit_2_folgt_latex_begin_align_frac_dq_dt_-_a_cdot_c_cdot_m_cdot_theta_._end_align_latex_8_im_experiment_fuellt_man_in_alle_gefaesse_die_gleiche_wassermenge._dann_kann_man_fuer_eine_bestimmte_uebertemperatur_diese_muss_fuer_alle_vier_gefaesse_gleich_sein_die_waermestroeme_anhand_der_abkuehlraten_latex_a_1_ldots_a_4_latex_vergleichen._gefaess_1_und_2_unterscheiden_sich_z.b._gerade_dadurch_dass_bei_gefaess_2_die_konvektion_ausgeschaltet_ist._die_differenz_der_waermestroeme_latex_begin_align_frac_dq_1{dt} - \frac{dQ_{2}}{dt} = \frac{dQ_{K}}{dt} \sim (a_{1} - a_{2})
\end{align*}$ </latex> (9)
ergibt den durch Konvektion verursachten Wärmestrom <latex>dQ_{K}/dt</latex>, der der Differenz der Abkühlraten proportional ist. Entsprechend kann man die anderen Wärmeströme <latex>dQ_{L}/dt</latex> (Wärmeleitung) und <latex>dQ_{S}/dt</latex> (Wärmestrahlung) ermitteln.
Aufgabenstellung
Füllen Sie die vier Gefäße mit jeweils gleicher Wassermenge der Temperatur von etwa <latex>70~^{\circ}\mathrm{C}</latex> und warten Sie bis die Thermometer in den Gefäßen nicht mehr weiter steigen. Messen Sie die Raumtemperatur <latex>T_{U}</latex> und kontrollieren Sie in regelmäßigen Abständen, ob diese konstant bleibt. Messen Sie zehn Mal in Abständen von fünf Minuten die Wassertemperaturen in allen vier Gefäßen.
Auswertung
- Stellen Sie <latex>\ln({\theta(t)}/{\theta(0)})</latex> als Funktion der Zeit <latex>t</latex> graphisch dar, und bestimmen Sie daraus die Abkühlraten <latex>a_{1}</latex> bis <latex>a_{4}</latex>.
- Berechnen Sie die Wärmeströme der vier Gefäße für eine Wassermenge der Masse <latex>m = 500~\mathrm{g}</latex> (spezifische Wärmekapazität von Wasser: <latex>c = 4.2~\mathrm{Ws/(gK)}</latex> und für eine Übertemperatur von <latex>50\,^{\circ}\mathrm{C}</latex>.
- Vergleichen Sie anhand dieser Wärmeströme die Effektivität der verschiedenen Isoliermaßnahmen.