Table of Contents
<texit info> author=laehnemann title=V6 </texit>
V6 - Versuchsanleitung
| V6 | ELEKTRISCHER WIDERSTAND |
|---|
Einleitung
Dieser Versuch soll Ihnen die elektrischen Größen Stromstärke, Spannung und Widerstand veranschaulichen und einfache Methoden ihrer Bestimmung aufzeigen.
Aus dem Umgang mit elektrischem Strom im Haushalt wird jeder Begriffe wie Spannung und Strom kennen; wäre es aber möglich, ein dlektrisches Gerät mit 2 kW Leistung an eind Steckdose anzuschliessen, die mit einer 10 A Sicherung abgesichert ist? Wieviel Strom (genauer Energie) wird es verbrauchen?
Im Organismus haben wir es mit einer Vielzahl von elektrischen Vorgängen zu tun: Nervenzellen beispielsweise besitzen ein negatives Ruhemembranpotential von 70-80 mV; die Nervenleitung ist das Resultat einer kurzfristigen Ionenverschiebung über die Zellmembran. Auch in der medizinischen Diagnostik beruhen zahlreiche Verfahren auf der Registrierung von Spannungen: EKG (Elektrokardiogramm), EEG (Elektroenzephalographie), ERG (Elektroretinographie), EMG (Elektromyographie).
Anwendungsbeispiele elektrischer Ströme in der Medizin: Defibrillation, Konversion, Herzschrittmacher. Widerstandsmessung der Haut: Hautgalvanische Reaktion (HGR) als psycho-vegetatives Maß.
Aufgabenstellung
1. Strom- und Spannungsmessung an zwei Widerständen
Es soll ein einfacher Stromkreis bestehend aus einer Spannungsquelle, einem oder zwei Widerständen <latex>R_{x1}</latex> bzw. <latex>R_{x2}</latex> und Messgeräten für Strom <latex>I</latex> und Spannung <latex>U</latex> aufgebaut werden (siehe Abbildung 1).
Die Messwerte für <latex>U</latex> und <latex>I</latex> in Abhängigkeit von <latex>R_x</latex> werden in tabellarischer Form (siehe Tabelle 1) im Protokoll notiert.
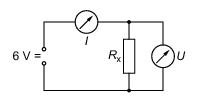
Abbildung 1: Stromkreis zur Bestimmung des Stroms <latex>I</latex> und des Spannungsabfalls <latex>U</latex> am Widerstand <latex>R_x</latex>.
2. Bestimmung des Widerstands
- Bestimmen Sie jeweils die Einzelwiderstände <latex>R_{x1}</latex> und <latex>R_{x2}</latex> aus Messungen von Strom <latex>I</latex> und Spannung <latex>U</latex>.
- Bestimmen Sie den Widerstand der in Serie (Reihe) geschalteten Widerstände <latex>R_{x1}</latex> und <latex>R_{x2}</latex> (siehe Abbildung 2A).
- Bestimmen Sie den Widerstand der parallel geschalteten Widerstände <latex>R_{x1}</latex> und <latex>R_{x2}</latex> (siehe Abbildung 2B).
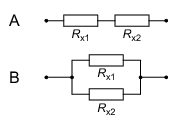
Abbildung 2: (A) Serienschaltung (Reihenschaltung) zweier Widerstände <latex>R_{x1}</latex> und <latex>R_{x2}</latex>. (B) Parallelschaltung zweier Widerstände <latex>R_{x1}</latex> und <latex>R_{x2}</latex>.
3. Potentiometerschaltung und Messung von Strom und Spannung an einer Glühlampe
Messen Sie den Strom <latex>I</latex> und die Spannung <latex>U</latex> anhand des in Abbildung 3 dargestellten Schaltkreises und erstellen Sie ein <latex>I(U)</latex>-Diagramm (Kennlinie). Wie verhält sich der Widerstand <latex>R</latex> der Metallfadenlampe mit zunehmender Temperatur?
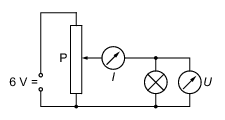
Abbildung 3: Schaltkreis zur Messung von Strom und Spannung an einer Glühlampe. P = Potentiometer.
4. Präzisionsmessung von Widerständen mit Hilfe der Wheatstoneschen Brücke
Es sollen zwei Widerstände <latex>R_x = R_{x1}</latex> und <latex>R_x = R_{x2}</latex> mit Hilfe des in Abbildung 4 dargestellten Schaltkreises bestimmt werden. Vergleichen Sie die Messergebnisse mit denen aus Aufgabenteil 1 und überlegen Sie wovon die Genauigkeit der beiden Messmethoden abhängt.
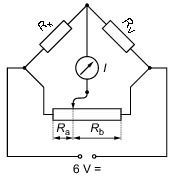
Abbildung 4: Schaltkreis zur Präzisionsmessung des Widerstands <latex>R_x</latex>. <latex>R_{V}</latex> ist ein Vergleichswiderstand.
Versuchsdurchführung
1. Zur Strom- und Spannungsmessung an Widerständen
Als Messgeräte werden im Praktikum sogenannte Multimeter verwendet. Mit ihnen können verschiedene elektrische Größen wie z.B. der Strom, die Spannung und auch Ohmsche Widerstände gemessen werden.
Beim Anschluss der Geräte achte man auf
- die Messgröße (Gleichstrom/Wechselstrom bzw. Gleichspannung/Wechselspannung) und den Messbereich. Man schätzt die Höhe der maximal zu erwartenden Spannungen und Ströme ab, wählt zunächst einen höheren Messbereich und kann später auf empfindlichere Bereiche umschalten. Der Messbereich entspricht der Anzeige bei Vollausschlag. Achten Sie auf die zugehörige Teilung (30 oder 100 Einheiten) und lesen Sie parallaxenfrei ab.
- die Polung der Messgeräte (Plus mit Plus, Minus mit Minus verbinden!). Zeichnen Sie die richtige Polung von Spannungsquelle und Messgerät in die Schaltskizze ein. Der Innenwiderstand bei der Spannungsmessung beträgt <latex>R_{i} = 40~\mathrm{k}\Omega/\mathrm{V}</latex>, also <latex>120~\mathrm{k}\Omega</latex> im 3-V-Bereich. Der Strom, der durch das Instrument fließt, ist daher im Vergleich zum Strom, der durch den Widerstand <latex>R_x</latex> fließt, zu vernachlässigen.
2. Zur Bestimmung des Widerstands
Die Ergebnisse aus den Aufgabenteilen 1 und 2 können in der folgenden Tabelle notiert werden.
Tabelle 1: Auswertung von Aufgabenteil 1 und 2:
| <latex>\qquad~U~\qquad</latex> | <latex>\qquad~I~\qquad</latex> | <latex>R_x = U/I</latex> | <latex>R_x</latex> | |
|---|---|---|---|---|
| <latex>R_x = R_{x1}</latex> | <latex>39~\Omega \pm 5~\%</latex> (Herstellerangabe) | |||
| <latex>R_x = R_{x2}</latex> | <latex>68~\Omega \pm 5~\%</latex> (Herstellerangabe) | |||
| Serienschaltung | ||||
| Parallelschaltung |
Verwenden Sie zur Berechnung des Gesamtwiderstands <latex>R_x</latex> im Falle der Serienschaltung von <latex>R_{x1}</latex> und <latex>R_{x2}</latex> (siehe Abbildung 2A) die Beziehung
<latex> $\begin{align*} R_x = R_{x1} + R_{x2} , \end{align*}$ </latex> (1)
und im Falle der Parallelschaltung von <latex>R_{x1}</latex> und <latex>R_{x2}</latex> (siehe Abbildung 2B) die Beziehung
<latex> $\begin{align*} \frac{1}{R_{x}} = \frac{1}{R_{x1}} + \frac{1}{R_{x2}}\, . \end{align*}$ </latex> (2)
3. Zur Potentiometerschaltung und Messung von Strom und Spannung an einer Glühlampe
Entscheiden Sie sich wie die Spannungsquelle gepolt werden soll und bestimmen Sie entsprechend der Skizze (Abbildung 3) wie die Polung der Messgeräte zu erfolgen hat.
Es sollen mindestens sechs Messwerte für Strom und Spannung ermittelt werden. Auf Millimeterpapier (in den Praktikumsräumen erhältlich) werden Achsen mit geeignetem Maßstab (Spannung <latex>U </latex> als Abszisse, Strom <latex>I </latex> als Ordinate) gewählt, die Messwerte eingetragen und eine Ausgleichskurve eingezeichnet.
4. Zur Präzisionsmessung von Widerständen
Bei der praktischen Ausführung der Wheatstoneschen Messbrücke sind <latex>R_{a}</latex> und <latex>R_{b}</latex> in Abbildung 4 durch einen Schiebewiderstand ersetzt (siehe Abbildung 5).
Er besteht aus einem <latex>100~\mathrm{cm}</latex> langen Draht mit verschiebbarem Schleifkontakt S, mit dem das Instrument auf Stromlosigkeit (<latex>I = 0</latex>) geregelt wird.
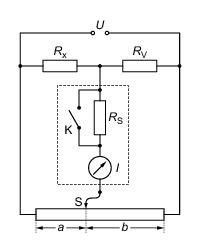
Abbildung 5: Schaltkreis zur Präzisionsmessung eines unbekannten Widerstands <latex>R_x</latex>. <latex>R_{V}</latex> ist ein bekannter Vergleichswiderstand, <latex>a</latex> und <latex>b</latex> sind Drahtlängen bei entsprechender Einstellung des Schleifkontakts S.
Dann gilt
<latex> $\begin{align*} R_x = R_{V} \cdot \frac{R_{a}}{R_{b}} = R_{V} \cdot \frac{a}{b} ,\end{align*} $ </latex> (3)
mit <latex>R_{a} = \rho \cdot a/A</latex> und <latex>R_{b} = \rho \cdot b/A</latex>. <latex>\rho</latex> ist der spezifische Widerstand des Schleifdrahts und <latex>A </latex> ist die Drahtquerschnittsfläche. Das Längenverhältnis <latex>a/b</latex> kann direkt auf einer zweiten Skala am Schiebewiderstand abgelesen werden. <latex>R_{S}</latex> ist ein im Instrument eingebauter Schutzwiderstand, der zur Feineinstellung durch den Taster K überbrückt werden kann. Als <latex>R_{V}</latex> benützen Sie einen Stöpsel-Rheostaten (siehe Abbildung 6). <latex>R_{V}</latex> ist dabei die Summe der nicht durch Stöpsel kurzgeschlossenen Widerstände. Stecken Sie niemals alle Stöpsel gleichzeitig ein, da sonst Kurzschlussgefahr droht!
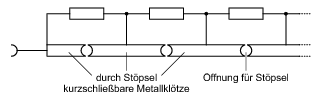
Abbildung 6: Schematische Darstellung eines Stöpsel-Rheostaten.
Bauen Sie die Brückenschaltung systematisch nach der Abbildung 5 auf. Stellen Sie den Schleifer S etwa auf Schleifdrahtmitte (<latex>a \approx b</latex>). Nach dem Einschalten wird das Strommessinstrument in der Regel bis zum Skalenende ausschlagen. Ziehen Sie so viele Stöpsel des Rheostaten, bis das Instrument nur wenig Stromfluss anzeigt. Mit dem Schleifer regeln Sie nun auf Stromlosigkeit (<latex>I = 0</latex>). Zur Empfindlichkeitserhöhung betätigen Sie den Taster K und gleichen fein ab. Tragen Sie die Werte für <latex>R_{V}</latex> und <latex>a/b</latex> in tabellarischer Form (siehe Tabelle 2) in Ihr Protokollheft ein.
Tabelle 2: Auswertung von Aufgabenteil 4:
| <latex>R_{V}</latex> | <latex>a/b</latex> | <latex>R_x = R_{V} \cdot a/b</latex> | <latex>R_x</latex> (aus Aufgabenteil 1) | |
|---|---|---|---|---|
| <latex>R_{x1}</latex> | ||||
| <latex>R_{x2}</latex> |
Stichwörter zum vorliegenden Versuch
Elektrischer Strom
Unter elektrischem Strom wird die Bewegung von elektrischen Ladungen verstanden. In Metallen sind Elektronen die Träger dieser Ladung. Eine Stromleitung ist auch durch Ionen möglich (z.B. in Lösungen und Gasen). Als technische Stromrichtung vereinbart ist die Richtung Pluspol <m>\right</m> Minuspol, also entgegengesetzt zur Bewegungsrichtung der Elektronen.
Stromstärke
Die Stromstärke <latex>I </latex> ist die durch eine Querschnittsfläche <latex>A </latex> pro Zeitintervall <latex>\Delta t</latex> fließende Ladungsmenge <latex>\Delta Q</latex>. Verändert sich der Strom während des Zeitintervalls <latex>\Delta t</latex>, so verkleinert man <latex>\Delta t</latex> so lange, bis der Strom als konstant angenommen werden kann. Die Stromstärke eines zeitlich veränderlichen Stroms in einem Leiter zur Zeit <latex>t </latex> ist also die Ladungsmenge <latex>{d}Q</latex>, die in einem infinitesimal kleinen Zeitintervall <latex>{d}t</latex> durch den Leiterquerschnitt fließt:
<latex> $\begin{align*} \mathrm{Elektrische~Stromstärke} = \frac{ \mathrm{Ladung} }{ \mathrm{Zeit} } \end{align*}$ </latex> (4)
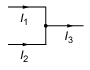
Knotenregel
An einem Verbindungspunkt von Leitern (Knoten) ist die Summe der zufließenden Ströme gleich der Summe der abfließenden Ströme (siehe Abbildung 9): <latex>I_{1} + I_{2} = I_{3}</latex>.
Messung der Spannung
Ein Spannungsmesser wird parallel zum Messobjekt geschaltet (siehe Abbildung 10). Ein Messgerät zur Messung von Spannungen sollte einen hohen Innenwiderstand <latex>R_{i}</latex> haben: <latex>R_{i} \gg R</latex>.
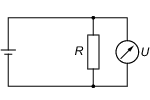
Abbildung 10: Messung des Spannungsabfalls <latex>U </latex> am Widerstand <latex>R </latex>.
Messung der Stromstärke
Ein Strommesser wird in Reihe zum Messobjekt geschaltet (siehe Abbildung 11). Messgeräte zur Messung der Stromstärke <latex>I </latex> sollten einen niedrigen Innenwiderstand <latex>R_{i}</latex> besitzen: <latex>R_{i} \to 0</latex>.
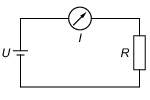
Abbildung 11: Messung der Stromstärke <latex>I </latex> in einem Stromkreis.
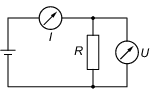
Gleichzeitige Messung von Stromstärke und Spannung
Bei der gleichzeitigen Messung von Stromstärke und Spannung in einem Stromkreis (siehe Abbildung 12) tritt ein systematischer Fehler bei der Strommessung durch den Innenwiderstand <latex>R_{i}</latex> des Spannungsmessers auf.
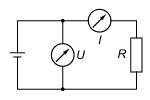
Welchen Nachteil hat die in Abbildung 13 dargestellte Schaltung zur gleichzeitigen Messung von Strom und Spannung?
Serienschaltung von Widerständen
Bei einer Serienschaltung von elektrischen Widerständen (siehe Abbildung 14) entspricht der Gesamtwiderstand <latex>R_{s}</latex> der Summe der Einzelwiderstände <latex>R_{i}</latex>:
<latex> $\begin{align*} R_{s} = \sum_{i=1}^{n} R_{i} = R_{1} + R_{2} + \ldots + R_{n} . \end{align*}$ </latex> (10)
Parallelschaltung von Widerständen
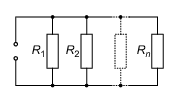
Parallel geschaltete Widerstände (siehe Abbildung 15) addieren sich reziprok:
<latex> $\begin{align*} \frac{1}{R_{p}} = \sum_{i=1}^{n} \frac{1}{R_{i}} = \frac{1}{R_{1}} + \frac{1}{R_{2}} + \ldots + \frac{1}{R_{n}} . \end{align*}$ </latex> (11)
Spannungsteiler
Betrachtet man den in Abbildung 16 dargestellten Schaltkreis, so folgt für die Stromstärke:
<latex> $\begin{align*} I = \frac{U_{0}}{R_{s}} = \frac{U_{0}}{R_{1}} + R_{2} = \frac{U_{2}}{R_{2}} = \frac{U_{1}}{R_{1}} \end{align*}$ </latex> (12)
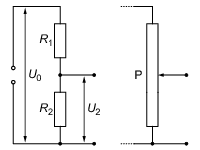
Abbildung 16: Spannungsteilung. P = Potentiometer.
Durch Umformung von (12) folgt dann:
<latex> $\begin{align*}\frac{U_{2}}{U_{0}} & = \frac{R_{2}}{R_{1} + R_{2}}
\frac{\mathrm{Teilspannung}}{\mathrm{Gesamtspannung}} & = \frac{\mathrm{Teilwiderstand}}{\mathrm{Gesamtwiderstand}}\end{align*}$ </latex> (13)
Werden <latex>R_{1}</latex> und <latex>R_{2}</latex> durch ein Potentiometer P (Widerstand mit variablem Abgriff) ersetzt, so kann <latex>U_{2}</latex> kontinuierlich zwischen Null und <latex>U_{0}</latex> variiert werden.
Wheatstonesche Brücke
Zeigt das Stromstärkemessinstrument der Wheatstoneschen Brücke (siehe Abbildung 17) keinen Strom (<latex>I = 0</latex>), dann besteht zwischen den Punkten P3 und P4 keine Potentialdifferenz. Die Beziehung zwischen den vier Widerständen ist dann besonders einfach, weil an <latex>R_x</latex> und <latex>R_{a}</latex> gleiche Spannungen <latex>U_x</latex> bzw. <latex>U_{a}</latex> abfallen: <latex>U_x = U_{a}</latex>. Ebenso gilt dann für <latex>R_{V}</latex> und <latex>R_{b}</latex>: <latex>U_{V} = U_{b}</latex>.
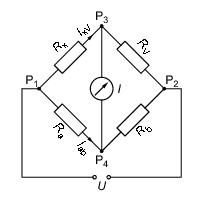
Abbildung 17: Wheatstonesche Brücke. <latex>I_{xV}</latex> und
<latex>I_{ab}</latex> sind die Ströme durch den oberen bzw. unteren
Zweig der Schaltung.
Die Definitionsgleichung für den elektrischen Widerstand liefert:
<latex> $\begin{align*}
U_x = U_{a} \to& I_{xV} \cdot R_x = I_{ab} \cdot R_{a}
U_{V} = U_{b} \to& I_{xV} \cdot R_{V} = I_{ab} \cdot R_{b}
& \multicolumn{1}{c}{\hrulefill}
\to& R_x / R_{V} = R_{a} / R_{b}
\end{align*}$ </latex>
Sind drei Widerstände bekannt, dann kann also der vierte (unbekannte) Widerstand im Fall der Stromlosigkeit nach <latex>R_x = R_{V} R_{a}/R_{b}</latex> berechnet werden.