Table of Contents
<texit info> author=gorgis title=FGS </texit>
FGS - New Versuchsanleitung
| FGS | FREIE GEDÄMPFTE SCHWINGUNGEN |
|---|
Einleitung
Schwingungen sind elementare Erscheinungen in allen Bereichen der Natur. Sie spielen eine herausragende Rolle bei den Naturerscheinungen selbst als auch bei vielen Messverfahren und technisch-methodischen Anwendungen. Von den Zweigen im Wind bis zu den Molekülen und Atomen im Verband des Kristallgitters gibt es ungezählte Beispiele für schwingungsfähige Systeme. Selbst der aufrechte Gang des Menschen kann formal als Schwingungsvorgang verstanden werden. Er neigt zu kippen, merkt's sogleich, und fängt mit einer geschickten Bewegung das schwindende Gleichgewicht wieder auf. Für gewöhnlich geht diese Regelschwingung recht unauffällig gut und nimmt nur im Falle fortgeschrittenen Rausches dramatischere Amplituden an. Mit diesem Versuch sollen die Eigenschaften eines schwingenden Systems am Beispiel eines elektrischen Schwingkreises untersucht werden, da die messtechnische Darstellung einschließlich der Dämpfung in diesem Fall besonders einfach ist.
Aufgaben
- (Vorversuch zur gemeinsamen Durchführung und sofortigen Auswertung durch die gesamte Gruppe): Aufbau eines Schwingkreises niedriger Frequenz aus einer Spule und einem Kondensator und einem Drehspulmessinstrument zum Nachweis der zeitlich periodischen Spannung am Kondensator. Messung der Schwingungszeit mit der Stoppuhr und der Amplitudenwerte am Messinstrument. Berechnung der Induktivität L aus der Kreisfrequenz (bei bekannter Kapazität) und des Verlustwiderstandes R aus der Dämpfungskonstanten.
- (Schwingkreis): Periodische Anregung eines Schwingkreises höherer Frequenz. Beobachtung und Messung des Schwingungsverlaufs mit dem Oszilloskop. Bestimmung der Parameter der Schwingung (Schwingungsdauer bzw. Kreisfrequenz und Dämpfungskonstante) und Vergleich mit den direkt gemessenen Daten der verwendeten Bauteile (Kapazität C des Kondensators, Induktivität L und Widerstand R der Spule).
Physikalische Grundlagen
Schwingungen
Damit ein physikalisches System schwingen kann, müssen bestimmte Voraussetzungen erfüllt sein. Es muss eine rücktreibende Größe geben (Federpendel: Federkraft; elektrischer Schwingkreis: Kondensatorspannung), durch die das System an eine Ruhelage gebunden ist, und es muss (wenigstens) zwei Erscheinungsformen für die Energie besitzen. Unter diesen Voraussetzungen ergibt sich ein zeitlich periodischer Vorgang, der als Schwingung bezeichnet wird. Charakteristisch für Schwingungsphänomene ist, dass der Energieinhalt des Systems ständig zwischen den beiden Erscheinungsformen hin- und herflutet.
Harmonische Schwingungen
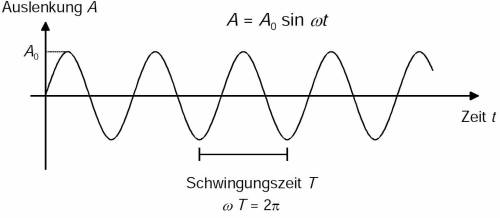
Die mathematisch einfachsten periodischen Funktionen sind die Sinus- und die Kosinusfunktion. Schwingungen, die diesen Funktionen folgen, werden als harmonische Schwingungen bezeichnet. Sie ergeben sich, wenn die rücktreibende Größe proportional zur jeweiligen Auslenkung aus der Ruhelage ist. Diese Bedingung ist zum Beispiel gut bei einer mechanischen Feder erfüllt (Hookesches Gesetz). In Abb. 1 ist der Verlauf einer sinusförmigen Schwingung wiedergegeben.
Die zeitliche Periode der Schwingung ist die Schwingungsdauer T, ihr Kehrwert die Frequenz f = 1/T . Die Frequenz gibt die Zahl der Perioden pro Zeit an; ihre Einheit 1/s wird 1 Hz (Hertz) genannt. Der Parameter im Argument der Sinus- und Kosinusfunktion ist ein Stauchfaktor in Richtung der Zeitachse, der das Verhältnis der mathematischen Grundperiode (2π) zur jeweiligen physikalischen Periode T darstellt:
Der Faktor \omega heißt Kreisfrequenz. Alle drei Angaben, T, f und ω sind äquivalente, gleichwertige Angaben zur Charakterisierung der (zeitlichen) Periode der Schwingung. Der Faktor gibt die größte Auslenkung wieder; er wird als Amplitude der Schwingung bezeichnet.
Federpendel und Schwingkreis
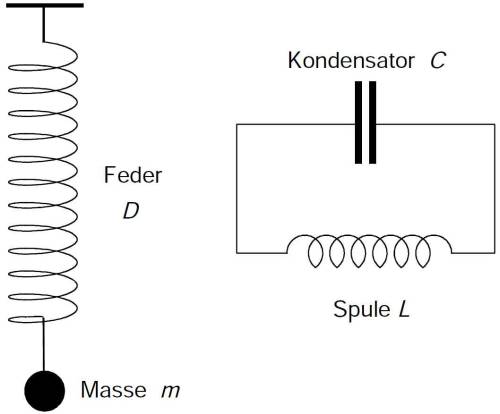
Der einfachste mechanische Oszillator ist das Federpendel (Abb. 2). Lenkt man den an eine Feder gebundenen Körper der Masse m ein Stück aus, so gewinnt er gegenüber der Ruhelage aufgrund der elastischen Verformung potentielle Energie. Beim Loslassen bewegt sich der Körper in Richtung Ruhelage zurück, und die potentielle Energie wird in kinetische Energie übergeführt. Wegen der Trägheit bewegt sich der Körper weiter über die Ruhelage hinaus und wird dann von der Feder abgebremst (verlangsamt), bis die gesamte Energie wieder in potentielle Energie übergegangen ist.
Der einfachste elektrische Oszillator ist ein Schwingkreis, der aus einer Spule und einem Kondensator besteht (Abb. 2 und 3). Ist der Kondensator aufgeladen, so bewirkt dessen Spannung einen Strom. Dieser baut in der Spule ein Magnetfeld auf, wobei die elektrische Feldenergie des Kondensators in magnetische Feldenergie der Spule umgewandelt wird. Nach dem Ladungsausgleich induziert das abnehmende Magnetfeld der Spule eine Spannung, die den Strom aufrechterhält und den Kondensator mit nunmehr umgekehrter Polarität wieder lädt. Bildhaft kann die Energie des Magnetfeldes wegen des zugrundeliegenden Stromes und der Eigenschaft, sich einer Stromänderung zu widersetzen, mit der kinetischen Energie und der Massenträgheit verglichen werden. Es ist jedoch zu beachten, dass dem nicht eine Trägheit der Bewegung der Elektronen zugrunde liegt, sondern die Eigenschaft von sich ändernden Magnetfeldern, der zugehörigen Stromänderung durch Induktion entgegenzuwirken.
Mathematische Behandlung (Differentialgleichung der Schwingung)
Ansätze der mathematischen Behandlung sind (u.a.) die Newtonsche Bewegungsgleichung (F = m a) beim Federpendel und die Kirchhoffsche Regel für Spannungen (∑U = 0; "Maschenregel") beim Schwingkreis. Die Kraft einer Feder ist ihrer Auslenkung x proportional (Hookesches Gesetz), der Proportionalitätsfaktor D wird Federkonstante genannt und beschreibt die Beschaffenheit der Feder:
Die Ladung Q eines Kondensators ist seiner "Größe" (der Kapazität C) und seiner Spannung UC proportional; Q = C UC. Daraus folgt mit der Definition des Stroms I = dQ/dt als Zusammenhang zwischen Strom und Spannung am Kondensator:
Durch Integration von (3) erhält man für die Spannung:
Der Spannungsabfall an einer Spule UL ist der zeitlichen Änderung des Stromes durch die Spule proportional. Aufgrund der Selbstinduktion widersetzt sich die Spule einer Stromänderung durch eine Gegenspannung (Lenzsche Regel), , die kompensiert werden muss (
):
Der Proportionalitätsfaktor heißt Selbstinduktionskoeffizient L der Spule (oder kurz Induktivität). Ausgehend von den obigen Zusammenhängen ergeben sich folgende Herleitungen der Schwingungsgleichungen für die beiden Systeme:
Federpendel
Schwingkreis
mit (4) und (5) und :
bzw. nach Ableitung nach t und Umstellung:
Beide Differentialgleichungen (6,7) haben mathematisch die gleiche Form. Als Lösung wird eine Funktion x = f(t) bzw. I = f(t) gesucht, deren zweite Ableitung nach der Zeit gleich der Funktion selbst ist, aber mit umgekehrtem Vorzeichen (und bis auf einen konstanten Faktor). Diese Bedingung erfüllen die Sinus- oder Kosinusfunktionen:
(8) Federpendel:
(9) Schwingkreis:
Durch Berechnung der zweiten Ableitungen und Vergleich mit (6) und (7) folgt, dass die Ansätze (8) und (9) genau dann Lösungen darstellen, wenn die Frequenzen bestimmte, durch die physikalischen Parameter D und m bzw. L und C gegebene Werte annehmen:
Federpendel
bzw.
woraus durch Vergleich mit (6) folgt:
(10)
Schwingkreis
bzw.
woraus durch Vergleich mit (7) folgt:
(11)
Die Systeme schwingen demnach mit ganz bestimmten, durch die systembestimmenden Größen D und m beziehungsweise L und C gegebenen Frequenzen (Eigenfrequenzen). Die Amplituden dagegen sind grundsätzlich beliebig (einschließlich und
für die ruhenden Systeme). Sie sind kein eigentliches Charakteristikum der Bewegungsform und gehen in die obigen Überlegungen zum Ansatz auch nicht ein.
Energieinhalt der Schwingung und Dämpfung
Das schwingende System besitzt einen bestimmten Energieinhalt. Einem Federpendel wird diese Energie z.B. durch die anfängliche Auslenkung der Feder zugeführt. Die dabei aufgewandte Arbeit ist (Kraft × Weg):
(12) bzw.
Danach ist die Amplitude ein Maß für den Energieinhalt der Schwingung (die Energie ist dem Quadrat der Amplitude proportional). Während der Schwingung findet eine laufende wechselseitige Umwandlung von potentieller Energie der Feder und kinetischer Energie der Masse statt. Für die Gesamtenergie gilt:
(13)
Einem Schwingkreis wird die Energie z.B. durch die anfängliche Aufladung des Kondensators zugeführt. Die dabei aufgewandte Arbeit ist:
(14)
Hier findet die wechselseitige Energieumwandlung zwischen der elektrischen Feldenergie des Kondensators und der magnetischen Feldenergie der Spule statt. Für die Gesamtenergie gilt in diesem Fall:
(15)
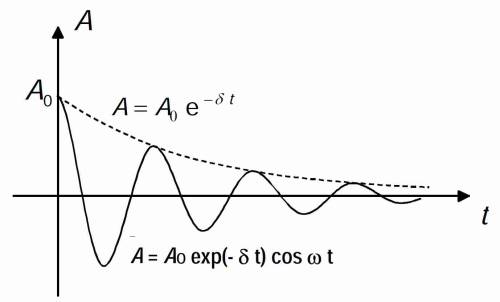
Verliert das System laufend Energie (durch Reibung beim Federpendel bzw. durch die Verlustwiderstände der Spule und der Verbindungsleitungen beim Schwingkreis), so nehmen die jeweiligen Amplituden ab. Dieser Vorgang wird als Dämpfung bezeichnet (Abb. 4). Die Abnahme der Amplitude ist im einfachsten Fall proportional zum Momentanwert (A) und zum Zeitintervall (dt), woraus eine Exponentialfunktion für das Abklingverhalten folgt:
(16)
Die vollständigen Schwingungsgleichungen mit den periodischen und den abklingenden Anteilen lauten dann:
(17) Federpendel:
(18) Schwingkreis:
Für den elektrischen Schwingkreis gilt folgender Zusammenhang zwischen der Dämpfungskonstanten , dem Verlustwiderstand R und der Induktivität L der Spule:
(19)
Oszilloskop (Elektronenstrahloszilloskop)
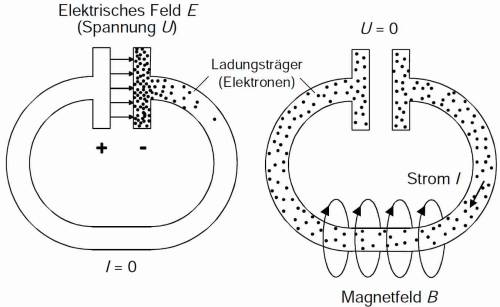
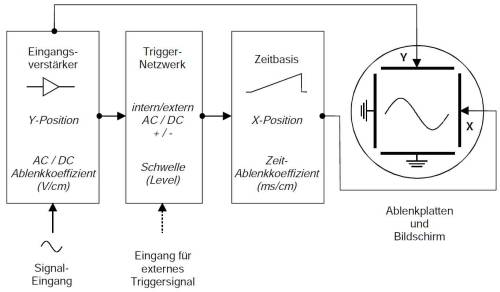
Das Oszilloskop ist ein wichtiges Instrument zur Beobachtung und Messung von zeitabhängigen, schnellen, wiederkehrenden elektrischen Signalen. Der vorliegende Versuch hat als ergänzendes Ziel die Einführung in dieses Gerät. Kernstück eines Oszilloskops ist eine Elektronenstrahlröhre mit einem Elektronenstrahl als praktisch trägheitslosem Zeiger. Zur Auslenkung des Elektronenstrahls wird die zu untersuchende Spannung an die Platten eines Ablenkkondensators innerhalb der Röhre gelegt, wobei die Elektronen durch die Kraft F = Q E im elektrischen Feld des Kondensators abgelenkt werden.
Oszilloskope besitzen zwei Ablenksysteme für die X- und für die Y-Richtung (Abb. 5). Zur Untersuchung von Spannung-Zeit-Verläufen wird das Signal über einen Eingangsverstärker an das Y-Ablenksystem gegeben. Zur Erzeugung einer Zeitachse besitzt das Oszilloskop eine Zeitbasis, die periodisch eine mit konstanter Geschwindigkeit anwachsende Spannung erzeugt (Sägezahnspannung). Diese Spannung wird an das X-Ablenksystem gelegt, wodurch der Strahl mit konstanter Geschwindigkeit über den Bildschirm läuft. Geschieht dies hinreichend schnell, so entsteht durch die Trägheit der Leuchtschicht des Bildschirms und des Auges eine durchgehende Linie. Ein Trigger-Netzwerk sorgt dafür, dass die Zeitbasis immer in dem Moment "angestoßen" wird, in dem das Signal am Y-Eingang erscheint und synchronisiert damit Signal und Zeitbasis. Für ein wiederkehrendes Signal erhält man auf diese Weise ein stehendes Bild auf dem Bildschirm des Oszilloskops.
Elementare Funktions- und Bedienelemente von Oszilloskopen
Bildschirm
- NTENS. und FOCUS: Regler zur Einstellung von Helligkeit und Schärfe des Bildpunktes (Achtung: eine zu große Helligkeit reduziert die Schärfe des Bildes).
- cm-Netz (DIV.) über dem Bildschirm zur quantitativen Ablesung der Messwerte.
Eingang (Eingangsverstärker)
- Y-POS.: Drehknopf zur Einstellung der horizontalen Lage des Bildes (oben/unten).
- VOLTS/DIV.: Drehschalter zur Einstellung der Eingangsempfindlichkeit (X-, Y-Ablenkkoeffizienten).
- VAR.: Drehknopf zur kontinuierlichen Einstellung der Eingangsempfindlichkeit. Achtung: Die Kalibrierung VOLT./DIV gilt nur dann, wenn VAR. am rechten Anschlag steht (Rastposition).
- DC-AC-GD: Kopplungsschalter; DC (direct current)= direkte, gleichstrommäßige Kopplung; AC (alternating current) = kapazitive, "galvanisch" getrennte Kopplung, bei der Gleichspannungsanteile unterdrückt werden; GD zur Einstellung des Nullpunktes (Nullinie).
- VERT. MODE: Schalter zur Wahl der Eingang-Betriebsart (Grundeinstellung: Alle Taster gelöst.)
Zeitbasis
- X-POS.: Drehknopf zur Einstellung der vertikalen Lage (rechts/links).
- TIME/DIV.: Drehschalter zur Einstellung des Maßstabes der Zeitachse (Zeit-Ablenkkoeffizient).
- VAR.: Drehknopf zur kontinuierlichen Einstellung der Zeitablenkung. Achtung: Die Kalibrierung TIME./DIV gilt nur dann, wenn VAR. am rechten Anschlag steht (Rastposition).
Trigger-Netzwerk
- TRIG.: Schalter zur Einstellung der Triggerart (DC / AC / HF = High- / LF = Low-Frequency / ∼ = Netzsynchronisation / ± = Steigung der Triggerflanke).
- EXT.: Externe Triggerung durch ein zusätzliches Synchronisations-Signal an der TRIG.INP.-Buchse.
- AT/NORM. – LEVEL: Schalter für automatische bzw. manuelle Triggerung. Drehknopf für Ansprechschwelle bei manueller Triggerung.
Versuchsdurchführung
Zu Aufgabe 1 (Demonstrationsversuch an einem Schwingkreis niedriger Frequenz)
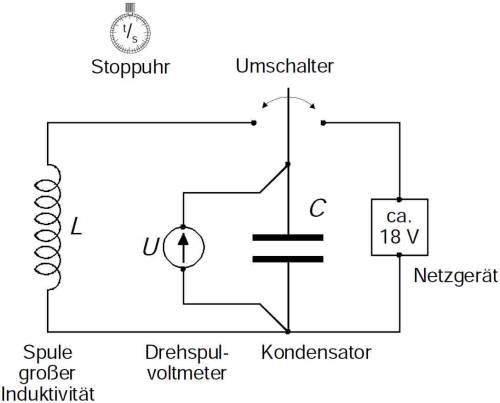
Aus einer Spule hoher Induktivität (L ≈ 600 H) und einem Kondensator großer Kapazität (C = (250 ± 50) μF) wird ein Schwingkreis niedriger Frequenz aufgebaut (f ≈ 0,3 Hz). Parallel zum Kondensator wird ein Voltmeter zum Nachweis der Spannung geschaltet. Der Aufbau entspricht Abb. 6. Der Kondensator kann über einen Umschalter durch ein Netzgerät aufgeladen (ausgelenkt) werden. Nach Umschalten wird die Folge der Spannungsamplituden mit dem Voltmeter und die Schwingungsdauer (möglichst viele Perioden!) mit der Stoppuhr gemessen. Die Dämpfungskonstante erhält man aus dem Verhältnis aufeinanderfolgender Amplituden (gleicher Richtung). Berechnen Sie dazu das Verhältnis aufeinander folgender Amplituden für die Zeiten t = t' und t = t' + T, und lösen Sie die dafür geltende Exponentialgleichung nach der Dämpfungskonstanten auf.
Steckbrett
Zum Aufbau einer übersichtlichen Schaltung ist ein Experimentier-Steckplatinensystem vorhanden (Steckbrett). Dabei ist eine belegte Buchse mit allen benachbarten Buchsen verbunden. Machen Sie sich vor Beginn der Messungen mit der Funktion des Steckbretts vertraut.
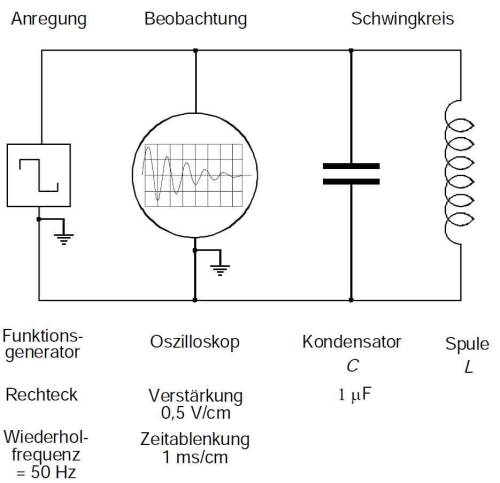
Zu Aufgabe 2 (Schwingkreis)
Mit Hilfe der Rechteckspannung eines Funktionsgenerators wird das Auslenken eines Schwingkreises und das Umschalten wie bei Aufgabe 1 periodisch und hinreichend schnell vorgenommen, so dass der Schwingungsverlauf bei höherer Frequenz als stehendes Bild auf dem Oszilloskop beobachtet werden kann. Die Schaltung entspricht Abb. 7. Es ist zu beachten, dass der Funktionsgenerator und das Oszilloskop jeweils mit einen Pol auf Erdpotential ("Erde") liegen und dort zusammengeschaltet werden müssen, um einen Kurzschluss zu vermeiden. Hinweise zu den Einstellungen an den Geräten sind im Platzskript angegeben, insbesondere auch zur Trigger-Einstellung am Oszilloskop. Als Messdaten werden Amplituden- und Zeitwerte direkt vom Bildschirm des Oszilloskops abgelesen. Zur Bestimmung der Frequenz wird die Zeit für eine größtmögliche Anzahl von Perioden abgelesen. Zur Bestimmung der Amplitudenwerte wird die Zeitachse zunächst soweit gestaucht, dass die Nullinie nach dem Ausschwingen beobachtet und auf die unterste Linie des cm-Netzes des Bildschirms geschoben werden kann. Nach erneuter Streckung der Zeitachse kann dann das Bild in X-Richtung jeweils verschoben und die Amplitudenwerte an der feineren Skala in der Mitte des Bildschirmnetzes mit höherer Auflösung abgelesen werden. Zur qualitativen Dokumentation des gesamten Schwingungsverlaufs soll zusätzlich das Oszilloskopbild maßstäblich auf das Karo-Netz des Laborhefts übertragen werden. Die Kapazität des Kondensators und die Induktivität der Spule sollen zum späteren Vergleich zusätzlich "direkt" mit einem digitalem R-C-L-Multimeter gemessen werden (Voltcraft 4090). Der Widerstand der Spule darf nicht mit diesem Multimeter, sondern muss mit dem Digitalmultimeter Metra Hit 12S bestimmt werden. Die Auswertung der Dämpfungskonstanten geschieht mit Hilfe einer logarithmischen Darstellung der Amplitudenwerte in Abhängigkeit von der Zeit.