Änderungen und Bemerkungenk

<texit info> author=Braun title=OPS Arbeitsversion </texit>

Als Licht (im engeren Sinne) bezeichnet man den sichtbaren Bereich des Spektrums elektromagnetischer Wellen mit Wellenlängen zwischen 700 nm (rot) und 400 nm (violett).

Licht entsteht beim Übergang angeregter Zustände der Elektronenhülle von Atomen, Molekülen oder Festkörpern in energetisch tiefer liegende Zustände oder den Grundzustand. Als Spektrum bezeichnet man die Zusammensetzung des Lichts nach Intensität und Wellenlänge bzw. Frequenz (Abb. 1). Freie Atome (z.B. in Gasen) emittieren eine relativ geringe Anzahl ganz bestimmter Frequenzen (Linien, Linienspektrum). Bei Molekülen ist die Zahl der Linien wesentlich größer. Bei Festkörpern können die Linien so dicht liegen, dass sich ein quasi-kontinuierliches Spektrum ergibt. Die Spektren sind charakteristisch für die emittierenden oder absorbierenden Systeme, und die Untersuchung der Spektren (Spektroskopie) liefert Informationen über deren Aufbau und Struktur. In den Anwendungen ist die optische Spektroskopie ein wichtiges Hilfsmittel zur Identifizierung von Substanzen (Spektralanalyse). Einen starken Aufschwung erlebte die optische Spektroskopie durch den Einsatz von Laser-Lichtquellen.

Abb. 1 Beispiele optischer Spektren

Zwei gebräuchliche Elemente, mit denen man optische Spektren erzeugen kann, sind das Prisma und das Beugungsgitter. Bei diesem Versuch kann wahlweise an einem Prismenspektrometer oder einem Gitterspektrometer gearbeitet werden.

Aufbau und Justierung eines optischen Spektrometers.

Aufnahme des Spektrums einer Quecksilberlampe (Ablenkwinkel <m>delta</m> in Abhängigkeit von der Wellenlänge <m>lambda</m>). Grafische Darstellung als Kalibrierkurve des Spektrometers.

Berechnung des Brechungsindex n des Prismas für die gelbgrüne Linie (<m>lambda</m> = 546 nm).

Spektroskopische Untersuchung einer unbekannten Lampe.

Qualitative Beobachtung des Quecksilberspektrums mit einem Beugungsgitter und Diskussion der charakteristischen Unterschiede.

Aufnahme des Spektrums einer Quecksilberlampe (Beugungswinkel <m>alpha</m> in Abhängigkeit von der Wellenlänge <m>lambda</m>).

==3. Gitterkonstante==: Berechnung der Gitterkonstanten an Hand der Linien des Quecksilberspektrums.

Spektroskopische Untersuchung einer unbekannten Lampe.

==5. Vergleich:== Qualitative Beobachtung des Quecksilberspektrums mit einem Prisma und Diskussion der charakteristischen Unterschiede.

Voraussetzung zur Versuchsdurchführung sind gute Kenntnisse über die Phänomene der Brechung (Brechung an einem Prisma; Zerlegung des Lichts; Dispersion), Beugung (Beugung und Interferenz; Beugung am Gitter) und Linsen (Brennpunkteigenschaft, Abbildung durch Linsen, Konstruktion der Abbildung). Dispersion und Ablenkung des Lichts durch ein Prisma Als Dispersion bezeichnet man die Abhängigkeit des Brechungsindexes eines Mediums von der Wellenlänge bzw. Frequenz. Damit ist ein Effekt gegeben, mit dem das Licht spektral zerlegt, d.h. nach unterschiedlichen Wellenlängenanteilen sortiert werden kann. Wegen der Dispersion hängt der Ablenkwinkel bei der Brechung (z.B. durch ein Prisma) von der Wellenlänge ab, so dass das Licht bei Durchgang durch ein Prisma in seine einzelnen Komponenten aufgespalten wird. 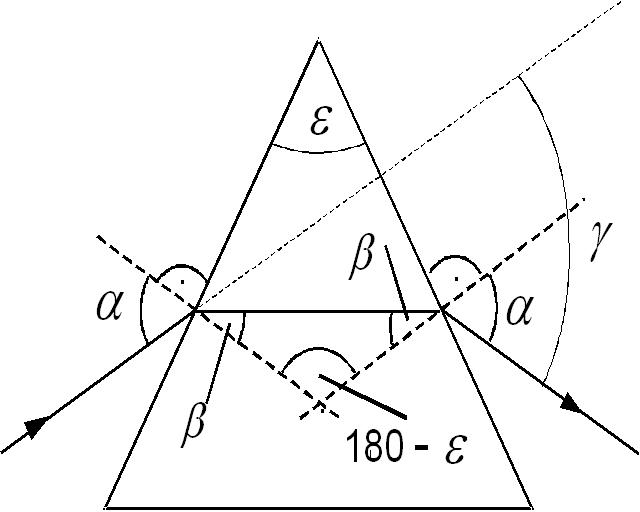Der Ablenkwinkel an einem Prisma ist neben dem Brechungsindex auch von der Richtung des einfallenden Lichtstrahls abhängig; er lässt sich aus dem Brechungsgesetz berechnen. Besonders einfache Verhältnisse erhält man, wenn der Lichtstrahl das Prisma symmetrisch durchläuft; so dass sich gleiche Ein- und Ausfallwinkel an den Grenzflächen ergeben (Abb. 2). Der Gesamt-Ablenkwinkel <m>gamma</m> wird in diesem Falle minimal (Minimal- ablenkung). Geometrisch ergibt sich aus Abb. 2:

Abb. 2 : Lichtbrechung an einem Prisma

<m 14> (1) beta=epsilon/2 (inneres Dreieck) </m>

          und

<m 14> (2) gamma=2(alpha-beta) </m>

          bzw.

<m 14> (3) alpha=(gamma+epsilon)/2 </m>

Daraus folgt mit dem Brechungsgesetz:

<m 14> (4) (sin alpha)/(sin beta)=c_0/c_p=n_p/n_0 </m>

         bzw.

<m 14> (5) n_p=n_0 sin((gamma+epsilon)/2)

/(sin epsilon/2), </m>

wobei <m>epsilon</m> der Winkel zwischen den brechenden Flächen und nP und n0 die Brechungsindizes des Prismas und des umgebenden Mediums sind (für Luft ist n0 = 1,0003).

An Kanten oder feinen Strukturen eines Objekts beobachtet man Beugungserscheinungen, d.h. Lichtintensität auch in geometrischen Schattenbereichen. Modellmäßig kann dies durch das Huygensschen Prinzip erklärt werden, einem Konstruktionsschema zur Betrachtung der Wellenausbreitung. Ein Wellenfeld kann danach in jedem Bereich in Ausgangspunkte von Elementarwellen zerlegt und die Intensitätsverteilung in einem anderen Bereich durch Überlagerung (Interferenz) dieser Elementarwellen konstruiert werden. Ein typisches Beispiel für die Anwendung dieses Prinzips ist die Erklärung der Beugungsdiagramme eines Spaltes, einer Lochblende oder eines Gitters. In diesem Versuch wird ein Gitter verwendet.

Ein Gitter ist eine regelmäßige Anordnung von Spalten (Beugungsgitter). Es werde von Licht einheitlicher Wellenlänge (monochromatisches Licht) und übereinstimmender Phasenlage beleuchtet (kohärentes Licht, ebene Welle). Hinter dem Gitter breitet sich das Licht entsprechend dem Huygensschen Prinzip von jedem der Spalte in alle Raumrichtungen aus, wobei sich die Intensitätsverteilung (z.B. auf einem Schirm) durch die Überlagerung (Interferenz) der einzelnen Strahlen ergibt.

Für eine Beobachtungsebene im Unendlichen ist die resultierende Helligkeit an einem betrachteten Punkt von der Phasenlage zueinander paralleler Wellenzüge abhängig, die sich dort überlagern. Sind die Wellenzüge von den Spalten um ein ganzzahliges Vielfaches (n = 0,1,2,…) der Wellenlänge gegeneinander verschoben, so verstärken sie sich gegenseitig (konstruktive Interferenz). Sind die Wellenzüge um eine halbe Wellenlänge (oder ein ungeradzahliges Vielfaches davon) verschoben, so löschen sie sich gegenseitig aus (destruktive Interferenz). Die Wegdifferenz benachbarter Wellenzüge wird als Gangunterschied bezeichnet. Ist der Abstand der Spalte in dem Gitter d (Gitterkonstante), so ergeben sich Interferenzmaxima, wenn der Gangunterschied der Helligkeitsbedingung n <m>lambda</m> genügt (Abb. 3):

<m 14> (6) d sin(alpha)=n lambda (n=0,1,2,….). </m>

Da die Richtung (Beugungswinkel <m>alpha</m>) der Interferenzmaxima nach (3) von der Wellenlänge abhängt, kann mit einem Gitter das Licht in seine spektralen Anteile zerlegt werden. Dabei treten Wiederholungen der zu einer Farbe (Wellenlänge) gehörenden Interferenzmaxima entsprechend der Folge der Laufzahl n auf, die als Interferenzmaxima der n-ten Ordnung bezeichnet werden. Zur experimentellen Realisation wird die Beobachtungsebene durch eine Sammellinse in das Endliche verlagert, wobei die Lichtstrahlen in der Brennebene der Linse vereinigt werden (Abb. 3), zur Erklärung der physikalischen Situation trägt die Linse aber nicht bei.

Abb. 3 Beugung und Interferenz an einem Gitter.

Da die Lichtstrahlen und Wellenfronten senkrecht aufeinander stehen, tritt der Winkel <m>alpha</m> sowohl als "Beugungswinkel" zur Ausbreitungsrichtung als auch als Winkel zwischen Gitterebene und Wellenfronten auf, der den Gangunterschied nach (3) bestimmt.

Zur quantitativen Messung der Ablenkung an einem Prisma oder einem Gitter ist paralleles Licht definierter Richtung erforderlich, das mit einem Kollimator erzeugt wird. Er besteht z.B. aus einer Sammellinse, in dessen Brennpunkt ein Spalt aufgestellt wird (Abb. 4). Der Spalt wird beleuchtet und stellt so eine (in einer Raumebene) punktförmige Lichtquelle dar. Zur Beobachtung des parallelen Lichtes wird ein auf unendlich eingestelltes Fernrohr benutzt, das den Spalt zunächst in die Brennebene des Fernrohrobjektivs (Zwischenbildebene) abbildet und in der es mit einem Okular (Lupe) vergrößert betrachtet wird. In der Zwischenbildebene ist zur Festlegung der Beobachtungsrichtung zusätzlich ein Fadenkreuz angebracht. Das Fernrohr ist schwenkbar um den Prismen- bzw. Gittertisch. Die Beobachtungsrichtung des Fernrohrs kann an einer Winkelskala mit Nonius abgelesen werden.

Abb. 4: Aufbau des Spektrometers

Der korrekte Aufbau und eine sorgfältige Justierung der Apparatur tragen zum Verständnis der optischen Komponenten und der Apparatur bei und sind eine wichtige Voraussetzung für eine einwandfreie Durchführung der Messungen.

Man beginnt zweckmäßigerweise mit der Justierung des Kollimators durch Autokollimation: Mit einem Spiegel wird das aus dem Kollimator kommende Licht auf die Kollimatorlinse zurückgeworfen und das dadurch erzeugte Bild des Spaltes auf den Spaltbacken selbst beobachtet. Aus der Brennpunkteigenschaft der Linse folgt, dass dieses Bild nur dann scharf ist, wenn der Spalt in der Brennebene der Linse steht. Diese Einstellung kann durch Verschieben des Spaltes kontrolliert werden.

Am Fernrohr wird zunächst bei entspanntem Auge das Fadenkreuz scharf eingestellt (Okular dazu von der optischen Bank nehmen und gegen einen erleuchteten Hintergrund halten). Dann wird bei wiedereingesetztem Okular der Spalt beobachtet und die Objektivlinse so justiert, dass man ein scharfes Bild erhält (Einstellung des Fernrohrs auf <m>infty</m>). Kriterium für eine gute Einstellung ist Parallaxenfreiheit, bei der das Bild des Spaltes genau in der Ebene des Fadenkreuzes liegt, so dass Spaltbild und Fadenkreuz sich bei seitlicher Bewegung des Auges nicht gegeneinander verschieben. Unter Umständen erscheint die eine Kante des Spaltbildes unscharf und überstrahlt, was gegebenenfalls an einer Schrägstellung des Spaltes zum Strahlengang liegen und durch leichtes Drehen des Spaltes korrigiert werden kann.

Danach wird der Prismen-/Gittertisch im Drehpunkt des Spektrometers waagerecht ausgerichtet (Stellschrauben).

Zum Schluss wird als erste Messeinstellung das Fadenkreuz präzise auf den Spalt eingestellt und der zugehörige Winkel an der Winkelskala abgelesen (1/100-Grad-Nonius; machen Sie sich mit dem Gebrauch des Nonius vertraut). Diese Einstellung (ca. 180 Grad) ist der Bezugswert, aus dem sich die anschließenden Messwerte (Ablenkwinkel, Beugungswinkel) durch Differenzbildung ergeben.

Das Prisma wird in Ablenkstellung gebracht (siehe Stellung des Prismas in Abb. 4) und so ausgerichtet, dass es vom Kollimator gut ausgeleuchtet wird und selbst wiederum das Fernrohrobjektiv gut ausleuchtet. Das Prisma muss dazu etwas aus der Mitte des Prismentisches heraus in Richtung der Basis verschoben werden. Das Spektrum wird dann durch das Fernrohr beobachtet und durch Drehen des Prismentisches für die gelbgrüne Linie mit <m>lambda</m> = 546 nm auf Minimalablenkung gestellt (dies ist eine wichtige Voraussetzung der Auswertung zu Aufgabe 3). Zum Schluss kann durch sehr leichtes Nachjustieren von Kollimatorlinse oder Objektiv die optische Abbildung optimiert werden.

Die Justierung der Apparatur darf danach für die gesamten Messungen nicht mehr verändert werden, damit die aufgenommenen Winkelwerte als Kalibrierung des Spektrometers für die spektroskopische Untersuchung der unbekannten Lampe ihre Gültigkeit behalten.

Die Messung besteht darin, alle beobachtbaren Linien des Hg-Spektrums zu identifizieren (siehe Darstellungen des Spektrums am Schluss des Skripts und im Platzskript) und die zugehörigen Winkel zu messen (Einstellungen des Fernrohrs). Orientieren Sie sich zunächst an den starken Linien (siehe grafische Darstellung des Spektrums) und vermessen Sie dann die schwächeren Linien. Zur Auswertung wird eine Kalibrierkurve anhand des Hg-Spektrums gezeichnet (Winkeleinstellungen gegen die Wellenlängen). Um eine hinreichende Genauigkeit zu erzielen, muss die Kalibrierkurve sehr sorgfältig angefertigt und eine Ausgleichskurve mit einem Kurvenlineal eingetragen werden.

Die Berechnung des Brechungsindexes des Prismas bei der Wellenlänge <m>lambda</m> = 546 nm erfolgt nach Gleichung (2). Der Winkel <m>epsilon</m> des Prismas ist im Platzskript angegeben.

Die Quecksilberlampe wird gegen eine der unbekannten Lampen ausgetauscht und deren Spektrum ebenfalls vermessen, wobei die Wellenlängen der Kalibrierkurve von Aufgabe 2 entnommen werden können. Die Messungen müssen sorgfältig durchgeführt werden, um gegebenenfalls die sehr ähnlichen Spektren von Cadmium und Zink (siehe Tabelle am Ende des Skripts) voneinander unterscheiden zu können. Zur Abschätzung der Messfehler ist neben der Ablesegenauigkeit der Winkelskala die Einstellreproduzierbarkeit der Linien zu berücksichtigen.

Das Prisma wird gegen das Beugungsgitter ausgetauscht. Beobachten, protokollieren und diskutieren Sie die charakteristischen Unterschiede im Spektrum (Reihenfolge der Linien, Auflösungsvermögen).

Beim Einsetzen des Gitters muss auf eine richtige Orientierung des Gitters (siehe Hinweise im Platzskript) und gut auf eine senkrechte Ausrichtung des Gitters zum Strahlengang geachtet werden. Diese Justierung kann wieder sehr genau durch Autokollimation, d.h. den Rückreflex des leicht verspiegelten Gitterträgers auf die Backen des Kollimatorspaltes kontrolliert werden.

Die Gitter sind so hergestellt, dass sich die größte Intensität und die besten Abbildungsverhältnisse in einer bestimmten Ablenkungsrichtung und Ordnung ergeben. Neben den eigentlichen Beugungsmaxima können durch Reflexionen sogenannte Geisterlinien entstehen, die aber an verfälschten Farben und ihrer unzutreffenden Lage erkannt werden können.

Zur Bestimmung der Gitterkonstanten wird das gesamte Hg-Spektrum in der 1.Ordnung und zusätzlich die gelbgrüne Linie (<m>lambda</m> = 546 nm) auch in der 2. Ordnung ausgemessen. Die Auswertung der Gitterkonstanten erfolgt numerisch nach Gleichung (3); für das Endergebnis der Gitterkonstanten ist ein Mittelwert zu berechnen.

Das Spektrum der unbekannten Lampe wird in der 1. Ordnung ausgemessen. Zur Abschätzung der Messfehler ist auch hier wieder neben der Ablesegenauigkeit der Winkelskala die Einstellreproduzierbarkeit der Linien zu berücksichtigen. Es sei darauf hingewiesen, dass die Einstellung auf einige Linien unter Umständen schwierig sein kann.

Das Beugungsgitter wird gegen das Prisma ausgetauscht. Beobachten, protokollieren und diskutieren Sie die charakteristischen Unterschiede im Spektrum (Reihenfolge der Linien, Auflösungsvermögen)

— Administrator 2009/04/10 14:10