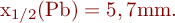Table of Contents
Einleitung
Radioaktive Stoffe und Präparate finden zunehmend Anwendung in vielen Bereichen von Wissenschaft und Technik. In der Medizin werden radioaktive Stoffe zur Diagnose und Therapie eingesetzt. Stoffwechselvorgänge und Funktionsabläufe können untersucht werden, indem man radioaktive Stoffe in ein Organ einbringt und deren örtliche und zeitliche Verteilung durch Messung der Strahlung sichtbar macht. In der Biologie und Chemie werden Transportvorgänge und Reaktionsverläufe durch Markierung mit radioaktiven Substanzen untersucht. Durch Bestrahlung können einfach und gezielt genetische Mutationen erzeugt werden. Altertums-, Erd- und Biowissenschaften machen Gebrauch von der 14C-Methode zur Altersbestimmung. In der Technik werden radioaktive Präparate für Überwachungs- und Regelzwecke und zur zerstörungsfreien Werkstoffprüfung eingesetzt.
Von radioaktiver Strahlung können erhebliche Gefahren für den Menschen ausgehen. Der Umgang mit radioaktiver Strahlung und radioaktiven Materialien ist daher gesetzlich geregelt, und die Vorschriften des Strahlenschutzes müssen genau beachtet werden!
Die Aktivität des in den Versuchen benutzten Neutronengenerators ist vergleichsweise gering. Seine Dosisleistung liegt in 1 m Abstand in der Größenordnung der natürlichen Strahlung, und eine zählende Belastung und ein zusätzliches Risiko sind bei der kurzfristigen Arbeit an den Versuchsplätzen nicht gegeben. Dennoch sind zur Arbeit an den Versuchsplätzen die grundsätzlichen Regeln der Strahlenschutzanweisung im allgemeinen Teil des Skripts zu beachten.
Ein wichtiges Ziel der Versuche Radioaktiver Zerfall und Gamma-Spektroskopie ist es, durch Vermittlung der Grundlagen der quantitativen Erfassung und Bewertung von Strahlenwirkungen (Dosimetrie) eine kritische Beurteilung von Strahlenwirkungen möglich zu machen.
1 Aufgaben
- (Dosisleistungsmessung. Gemeinsame Aufgabe zur sofortigen Auswertung): Messung der natürlichen Äquivalentdosisleistung und (zum Vergleich) der Äquivalentdosisleistung des 60Co-Präparats in 0,3 m Abstand. Umrechnung der Einheit der gemessenen Werte (
Sv/h) in Sv pro Jahr.
- (Kalibrierung des Spektrometers): Aufnahme der
-Spektren beim Zerfall von 60Co, 137Cs und 241Am mit Linien bekannter Energie. Grafische Darstellung (Energie gegen Kanalnummer) und Anpassung einer Kalibrierkurve.
- (e+-e--Vernichtungsstrahlung): Bestimmung der Energie der e+-e--Vernichtungsstrahlung am 22Na-Präparat und Vergleich mit der Einsteinschen Beziehung.
- (Auflösungsvermögen): Bestimmung des relativen Auflösungsvermögens des Spektrometers für die 0,662-MeV-Linie von 137Cs.
- (Absorptionsgesetz): Überprüfung des Absorptionsgesetzes für
-Strahlung und Bestimmung der Halbwertsdicke von Blei für die 0,662-MeV-Strahlung von 137Cs.
2 Physikalische Grundlagen
2.1 Radioaktiver Zerfall
Atomkerne sind aus Protonen und Neutronen aufgebaut. Die Zahl der Protonen (P) ist gleich der Anzahl der Elektronen in der Hülle des Atoms; sie bestimmt das Element und die chemischen Eigenschaften. Die Zahl der Neutronen (N) ist bei leichten Kernen etwa gleich, bei schweren Kernen größer als die Protonenzahl. Die Summe aus P und N heißt Nukleonenzahl A. Von allen Elementen existieren Modifikationen mit unterschiedlicher Neutronenzahl, die Isotope genannt werden. Die Kennzeichnung eines speziellen Isotops geschieht durch Angabe des Buchstabensymbols für das Element und die Massenzahl. Aus diesen Angaben gehen auch die Protonenzahl P und die Neutronenzahl N hervor, z.B.:

Isotope mit vom obigen "Gleichgewichtszustand" abweichender Neutronenzahl sind energetisch instabil und wandeln sich spontan unter Aussendung von Teilchen um (Radionuklide; radioaktiver Zerfall). Die Umwandlungen erfolgen durch -Zerfall oder
-Zerfall (
;
; EC = electron capture), wobei sich die Protonenzahlen und damit die chemische Natur der Atome ändern. Nach dem Zerfall befinden sich die Folgekerne im Allgemeinen in einem angeregten Zustand höherer Energie, aus dem sie unter Aussendung von elektromagnetischer Strahlung (
-Strahlung) in den Grundzustand übergehen.
-Zerfall: Bei schweren Kernen wird ein ganzes Bruchstück aus zwei Protonen und zwei Neutronen (He-Kern,
-Teilchen) abgespalten, wodurch sich das Verhältnis von Neutronenzahl zu Protonenzahl verändert, z.B.:

Der * beim Folgekern 232Th kennzeichnet, dass sich der Kern in einem angeregten Zustand befindet.
-Zerfall: Beim
-Zerfall wandelt sich ein Neutron in ein Proton um oder umgekehrt. Dabei werden Elektronen (
-Strahlung) oder Positronen (
-Strahlung) und zusätzlich sogenannte Antineutrinos (
) oder Neutrinos (
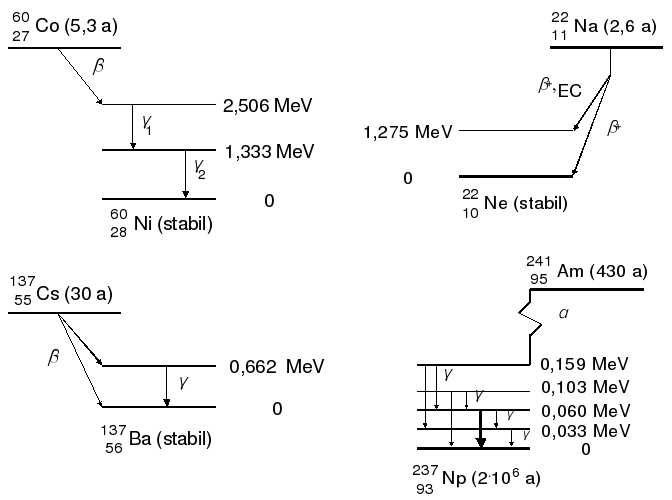
 ) emittiert:
) emittiert:


- EC (Elektroneneinfang; electron capture): Der Elektroneneinfang entspricht einem
-Zerfall in umgekehrter Richtung, wobei ein Kernproton ein Hüllenelektron einfängt (s-Elektronen haben eine zwar kleine, aber nicht verschwindende Aufenthaltswahrscheinlichkeit am Ort des Kerns):
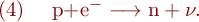
-Strahlung: Nach radioaktiven Umwandlungen befinden sich die Folgekerne häufig in energetisch angeregten Zuständen (*; s.o.). Sie gehen mit unterschiedlichen Übergangswahrscheinlichkeiten (bzw. mittleren Lebensdauern oder Halbwertszeiten als äquivalenten Parametern) weiter in den Grundzustand über, wobei die freiwerdende Energie in Form von (elektromagnetischer)
-Strahlung ausgesandt wird, z.B.:

2.2 Dosimetrie
Die Dosimetrie erfasst quantitativ die physikalischen und biologisch-physiologischen Wirkungen von Strahlung auf organische Materie; sie ist ein für Medizin und Biologie wichtiges Arbeitsgebiet. Bei den Betrachtungen muss zwischen Ursache und Wirkung unterschieden werden. Ursachen von Strahlenbelastungen sind radioaktive Quellen, deren Stärke durch ihre Aktivität, d.h. die Anzahl der Zerfälle pro Zeit in der Maßeinheit 1 Bq (Bequerel) = 1 Zerfall pro Sekunde gemessen wird.
Die Wirkungen beziehen sich immer auf eine Probe im Strahlungsfeld, die eine bestimmte Strahlungsmenge pro Masse, die Dosis, durch Absorption aufnimmt: gibt es nichts oder Niemanden in der Nähe eines Strahlers, so gibt es auch keine Folgen. Die physikalisch-makroskopischen Folgen sind zunächst ein im Probekörper deponierter Betrag an Energie. Die primären mikroskopisch-chemischen Folgen sind Ionisationen oder andere komplizierte Veränderungen der chemisch-atomaren oder molekularen Struktur der Probensubstanz, die dann Ursache für nachfolgende physiologische und biologische Strahlenschädigungen sind.
Bringt man eine Probe (z.B. Muskel- oder Weichteilgewebe als organischen Körper) in ein radioaktives Strahlungsfeld, so wird ein Teil der Strahlungsenergie absorbiert, während ein anderer Teil die Probe oder den Körper ohne Wechselwirkung, und damit ohne Schädigung, durchläuft.
Als Maß für die aufgenommene (absorbierte) Strahlung wird zunächst die Energiedosis als absorbierte Energie pro Masse definiert. Dosisangaben beziehen sich immer auf eine bestimmte Probe und einen bestimmten Stoff als Probensubstanz. Sie charakterisieren aber auch die Stärke eines Strahlungsfeldes durch die Betrachtung, dass diese Energie aufgenommen würde, wenn sich die entsprechende Probe am Ort dieses Strahlungsfeldes befände:

Die Einheit der Energiedosis ist:
![LaTeX
\mathrm{(7)} \ \ \ [D_E] = 1 \frac{\mathrm{J}}{\mathrm{kg}} = 1 \mathrm{Gy} \ \ \mathrm{(Gray)}.](/praktikum/lib/exe/fetch.php?media=wiki:latex:/img6a0c068010198c44dbdb16ec303808af.png)
Die Energiedosis ist schwer direkt messbar, da die bei praktischen Betrachtungen gegebenen Energiemengen sehr gering sind (eine für den Menschen 100-%-ig letale Strahlendosis beträgt etwa 8 J/kg. Vergleiche: Zur Temperaturerhöhung von Wasser um 1 K sind 4200 J/kg erforderlich, d.h. die Energie einer tödlichen Strahlendosis entspricht der Wärmemenge eines Schluckes Kaffee! Physikalisch und messtechnisch gut nachweisbar ist das Ionisationsvermögen radioaktiver Strahlung und als praktische Messgröße wird daher zusätzlich die Ionendosis
mit Luft als Probensubstanz definiert:
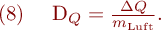
Die Einheit ist:
![LaTeX
\mathrm{(9)} \ \ \ [D_Q] = 1 \frac{\mathrm{C}}{\mathrm{kg_{Luft}}} = 1 \frac{\mathrm{As}}{\mathrm{kg_{Luft}}}.](/praktikum/lib/exe/fetch.php?media=wiki:latex:/img1b15700b8fa041650eb707617a8e725e.png)
Die Ionendosis kann direkt mit sogenannten Ionisationskammern gemessen werden.
Der Zusammenhang zwischen Energie- und Ionendosis hängt einerseits vom Probenmaterial und andererseits von der Quantenenergie der Strahlung ab. Für Muskel- und Weichteilgewebe gilt in guter Näherung in weiten Bereichen unabhängig von der Quantenenergie:

Die biologische Strahlenwirkung wird darüber hinaus auch von der Strahlenart bestimmt, was in einem zusätzlichen Faktor für die relative biologische Wirksamkeit (RBW-Faktor) zum Ausdruck gebracht wird (Tab. 1):
| Strahlenart | RBW-Faktor |
|---|---|
| | 1 |
| langsame Neutronen | 5 |
| | 10 |
| Röntgenstrahlung | 5…10 |
Tab.1 RBW-Faktoren
Die Energiedosis multipliziert mit dem RBW-Faktor ergibt dann die wirkungsrelevante Äquivalentdosis
= RBW
.
Die Einheit der Äquivalentdosis ist, genau wie die der Energiedosis, 1 J/kg; sie wird zur Unterscheidung jedoch 1 Sv (Sievert) genannt:
![LaTeX
\mathrm{(11)} \ \ \ [D_{Ä}] = 1 \frac{\mathrm{J}}{\mathrm{kg}} = 1 \mathrm{Sv} \ \ \mathrm{(Sievert)}.](/praktikum/lib/exe/fetch.php?media=wiki:latex:/imgf6d63788edbab185853a4ad93a4d4e37.png)
Neben den Dosiswerten tritt insbesondere als praktische Messgröße vielfach die auf die Zeit bezogene Dosis, d.h. die Dosisleistung auf.
2.3 Quantenenergie und Zerfallschema
Die Atomkerne besitzen, genauso wie die Elektronenhülle, nur diskrete mögliche Anregungszustände, so dass bei Umwandlungsprozessen oder Übergängen innerhalb eines Kerns bestimmte Energiemengen umgesetzt werden. Diese Einzelenergie der Teilchen oder der Strahlungsquanten beim radioaktiven Zerfall wird als Quantenenergie der Strahlung bezeichnet. Die in der Kernphysik übliche Energieeinheit ist 1 eV (Elektronenvolt); sie ist die Energie, die eine Elementarladung ( 1,602 10-19 C) beim Durchlaufen einer Spannung von 1 V gewinnt:
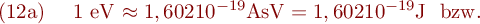
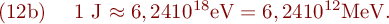
Ein radioaktiver Zerfall kann übersichtlich in einem Zerfallsschema dargestellt werden, das die Grund- und angeregten Zustände der Kerne (Niveaus) als Linien und die möglichen Umwandlungen oder Übergänge als Pfeile enthält. Die Zerfallsschemata der beim vorliegenden Versuch benutzten radioaktiven Strahler sind in Abbildung 1 dargestellt.
!! Abb.1: Zerfallsschemata von 60Co, 22Na, 137Cs und 241Am. !!

2.4 Gamma-Spektren
Die bei Übergängen innerhalb eines angeregten Kerns zu erwartenden Linien im -Spektrum der verschiedenen Isotope gehen aus den o.a. Zerfallsschemata hervor. Die Hauptlinien sind (Tabelle 2):
| Nuklid | Übergangsenergie |
|---|---|
| 60Co | 1,173 MeV |
| 1,333 MeV | |
| 137Cs | 0,662 MeV |
| 241Am | 0,060 MeV |
Tab. 2 -Übergangsenergien der verwendeten Isotope
Die Hauptlinie von 22Na entspricht keinem -Übergang, sondern stellt eine Vernichtungsstrahlung dar. Sie entsteht, wenn das beim Zerfall von 22Na ausgesandte Antiteilchen Positron (e+ oder
) auf ein Elektron (e- oder
) als zugehöriges Teilchen stößt, wobei die Materie entsprechend der Einsteinschen Beziehung in Strahlungsenergie umgesetzt wird:

Bedingt durch den Impulserhaltungssatz werden bei dem Prozess zwei -Quanten emittiert, so dass rechnerisch jedes
-Teilchen in ein
-Quant übergeht. Die Massen von Elektron und Positron stimmen überein; der Wert für
und für die Lichtgeschwindigkeit c ist im Abschnitt Konstanten zu finden.
2.5 Absorption von Gamma-Strahlung
Die Absorption, d.h. die Schwächung von Strahlung beim Durchgang durch Materie, kann wegen der gequantelten Natur der Strahlung in einer einfachen Vorstellung als Zufallsprozess verstanden werden, bei dem innerhalb einer Schicht dx des Absorbermaterials ein betrachtetes Strahlungsquant durch einen Wechselwirkungsvorgang mit einer bestimmten Wahrscheinlichkeit () aus dem Strahlengang entfernt wird. Für einen Teilchen- bzw. Quantenstrom I (Quanten pro Zeit, Zählrate im Experiment) folgt daraus als Ansatz für die Abnahme dI:

Als Lösung der Differentialgleichung (14) wird eine Funktion I(x) gesucht, die (bis auf einen Proportionalitätsfaktor) mit ihrer Ableitung übereinstimmt. Diese Bedingung erfüllt die e-Funktion, und die Lösung ist:
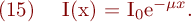
Der Absorptionskoeffizient wird als linearer Schwächungskoeffizient bezeichnet und hängt von der Dichte des Absorbermaterials und der Quantenenergie der Strahlung ab. Eine äquivalente Angabe für den Schwächungskoeffizienten ist die Halbwertsdicke x1/2, die aus (15) berechnet werden kann:

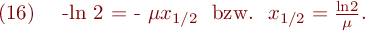
Für die Absorption sind mikroskopisch drei Wechselwirkungsprozesse verantwortlich:
- Photoeffekt: Das
-Quant wird vollständig gestoppt. Die gesamte
-Energie wird auf ein Hüllenelektron übertragen, das dadurch aus der Elektronenhülle herausgeschlagen wird. Das ionisierte Atom bleibt in einem energetisch angeregten Zustand zurück und reorganisiert sich unter Aussendung von Licht- und Röntgenstrahlung.
- Compton-Effekt: Das
-Quant wird lediglich an einem Hüllenelektron gestreut. Es gibt nur einen Teil seiner Energie an das Elektron ab und läuft selbst mit geringerer Energie (
weichere Strahlung) weiter. Die Folgen für das getroffene Atom sind die gleichen wie beim Photoeffekt. Der Compton-Effekt spielt bei Bestrahlungs- und Strahlenschutzproblemen eine entscheidende Rolle, weil durch ihn hochenergetische Strahlung, die eine geringere Absorptionswahrscheinlichkeit hat, in niederenergetische Strahlung mit höherer Absorptionswahrscheinlichkeit konvertiert wird. Dadurch verteilt sich die Dosis nicht gleichmäßig über eine Probe, sondern hat ein Maximum nach einer bestimmten Eindringtiefe (Aufbaueffekt).
- Paarbildungseffekt: Bei höheren Energien kann sich die Energie eines
-Quants in der Nähe eines Atomkerns spontan materialisieren, wobei ein Elektron-Positron-Paar erzeugt wird (umgekehrter Effekt zur Vernichtungsstrahlung).
2.6 Aufbau des Gamma-Spektrometers
Geräte zum Strahlungsnachweis nennt man Strahlungsdetektoren. Die meisten Detektoren nutzen das Ionisationsvermögen der Strahlung aus (z.B. Geiger-Müller-Zählrohre; siehe Versuch Radioaktiver Zerfall). Beim vorliegenden Versuch wird als Detektor ein Szintillationsdetektor (siehe Abbildung 2) eingesetzt, dessen Wirkungsweise auf dem Photoeffekt beruht (s.o.). In einem NaJ-Kristall wird das -Quant durch ein Hüllenelektron absorbiert (Photoeffekt), das aus dem Molekülverband herausgeschlagen wird und sich als freies Elektron im Kristall bewegt. Bei der anschließenden Abbremsung des Elektrons werden zahlreiche Atome optisch angeregt, die bei ihrer Rückkehr in den Grundzustand Licht aussenden. Das Licht fällt auf eine Photokathode, wo es wiederum durch Photoeffekt freie Elektronen auslöst. Diese Elektronen werden in einen Sekundärelektronenvervielfacher lawinenartig verstärkt und verursachen einen elektrischen Impuls, der anschließend elektronisch weiterverstärkt wird. Das gesamte System arbeitet linear, d.h. die Höhe des Ausgangsimpulses des Systems ist proportional zur Energie des auslösenden
-Quants.
!! Abb. 2: Szintillationszähler !!

Zur Aufnahme des Spektrums eines Strahlers müssen die Impulse nach ihrer Höhe (Energie) sortiert und zur Bestimmung der Anzahl bzw. Intensität gezählt werden. Diese Funktion übernimmt ein Vielkanal-Impulshöhenanalysator. Das System besteht aus einem Impulshöhendetektor, der die Impulshöhen misst und in digitalisierter Form einem diskreten Wertebereich von Impulshöhenstufen zuordnet (z.B. zwischen 0 und 256). Dem nachgeschaltet ist ein Zähler mit 256 Zählstellen (Kanälen), in denen die Anzahlen der Impulse verschiedener Höhe gezählt werden. Als Inhalt der Kanäle erhält man so die Verteilung der Intensität (Kanalinhalt) über der Energie (impulshöhenproportionale Kanalnummer). Das Funktionsdiagramm eines Vielkanal-Impulshöhenanalysators ist in Abb. 3 wiedergegeben.
!! Abb.3: Vielkanalanalysator. !!
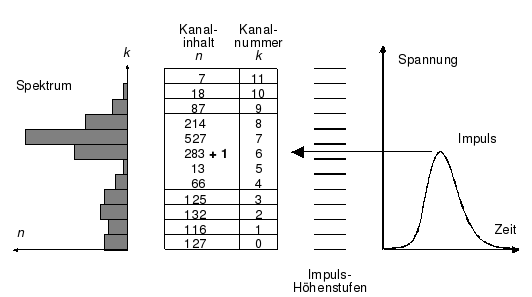
Die Zähler sind auf einem PC eingerichtet, mit dem das Spektrum gespeichert und digital bearbeitet werden kann (grafische Darstellung, Ausgabe der Daten, Summieren von Bereichen des Spektrums und Berechnung der Zählrate unter Berücksichtigung der Messzeit).
2.7 Auflösungsvermögen
Als Auflösungsvermögen eines Messsystems bezeichnet man die kleinste Differenz zweier Werte, die noch getrennt wahrgenommen werden können (siehe auch Abschnitt Fehlerrechnung); das relative Auflösungsvermögen
bezieht sich, entsprechend dem relativen Fehler, zusätzlich auf die Messgröße selbst. Bei dem vorliegenden Spektrometer geht es um das
-Energieauflösungsvermögen:
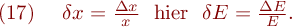
Bei Kernstrahlungsmessgeräten ist es üblich, als kleinste auflösbare Differenz die volle Breite bei halbem Maximum (Halbwertsbreite) der Linie eines Spektrums anzusetzen.
2.8 Fehler von Zählgrößen beim radioaktiven Zerfall
Der radioaktive Zerfall verhält sich als spontaner Prozess zufällig und unterliegt statistischen Gesetzmäßigkeiten. Die Anzahl der Zerfälle in einem bestimmten Zeitintervall z.B. ist normalverteilt, wobei die Standardabweichung als Fehler des einzelnen Messwerts gleich der Wurzel aus der Anzahl der registrierten Ereignisse N ist:

Beispiel: Werden in 10 s 1327 Ereignisse registriert, so ist der Fehler , das Ergebnis also N = (1327
37) Ereignisse (bzw. als Endergebnis korrekt gerundet: N = (1,33
0,04) 103 Ereignisse). Werden Ereignisse zusammengefasst (addiert) oder voneinander abgezogen (Subtraktion von Untergrund), so gilt die Wurzelregel in beiden Fällen für die Summe der Ereignisse; d.h.

(Der scheinbare Widerspruch zu den in der Anleitung Fehlerrechnung angegebenen Fehlerfortpflanzungsregeln erklärt sich daraus, dass im Rahmen dieses Praktikums aus Vereinfachungsgründen die Fehlerregeln für den Maximalfehler benutzt werden, die die statistische Natur der Fehler nicht berücksichtigen).
3 Versuchsdurchführung
Zu Aufgabe 1 (Dosisleistungsmessung)
Zur Messung der Äquivalentdosisleistung ist ein in Sv/h kalibriertes Äquivalentdosisleistungsmessgerät vorhanden. Besondere Bedienungshinweise sind am Messplatz zu finden.
Bedienung des Spektrometers (Aufgaben 2-5)
Die Bedienung der Einzelgeräte (Hochspannungsversorgung, Impulshöhendetektor, PC als Vielkanalzähler) geht weitgehend aus der Beschriftung an den Geräten bzw. den Programm-Menüs hervor; zusätzliche Einstellhinweise sind im Platzskript angegeben. Es wird empfohlen, vor Beginn der Messungen ausgiebig mit den Geräten zu experimentieren, um die Funktionsweise und das Verhalten des Aufbaus gut zu verstehen. Neben den physikalischen Inhalten stellt die Apparatur ein System dar, an dem der statistische Charakter von Messungen anschaulich beobachtet werden kann.
Zu Aufgaben 2 und 3 (Kalibrierung und Messung der Energie der Vernichtungsstrahlung)
Die Spektren der verschiedenen Isotope werden aufgenommen und die Lage der Linien (Kanalnummer ) mit Hilfe der Funktion Impulszahl aufgesucht, wobei die Lage entweder durch das Maximum oder besser durch den Kanal, der die Linie in zwei flächengleiche Hälften teilt (Median, visuelle Beurteilung), gekennzeichnet ist. Die Messzeit für die einzelnen Spektren ist so zu wählen, dass sich eine hinreichende Qualität ergibt (statistische Genauigkeit). Die gesamte Aufnahme eines Spektrums und die Bestimmung der Lage einer Linie ist exemplarisch zu wiederholen, um aus der Reproduzierbarkeit eine Schätzung für den Fehler zu gewinnen.
- Wichtig: Zum Nachweis der vergleichsweise niederenergetischen 0,06-MeV-Strahlung von 241Am muss die Untergrund-Einstellung (Ansprechschwelle; Menü Optionen) auf Kanal 1 oder 2 herabgesetzt werden.
Zur Auswertung wird die Lage der Linien gegen die bekannten Energiewerte grafisch dargestellt und eine Kalibrierkurve (Kurvenlineal!) an die Messwerte angepasst. Anhand der Kalibrierkurve kann dann die Energie der Vernichtungsstrahlung (Spektrum von 22Na) bestimmt werden. Um ein anschauliches Bild eines Spektrums im Protokoll zu haben, soll zusätzlich der Verlauf des gesamten Spektrums von 137Cs vom Bildschirm skizziert werden.
Zu Aufgabe 4 (Auflösungsvermögen)
Zur Bestimmung des Auflösungsvermögens des Spektrometers wird die gesamte 0,662-MeV-Linie von 137Cs punktweise ausgelesen (Funktion Impulszahl) und grafisch dargestellt. An die Punkte wird eine Glockenkurve als Ausgleichskurve angepasst und die volle Breite bei halbem Maximum abgelesen. Da Kanäle und Energien näherungsweise proportional zueinander sind, kann das relative Auflösungsvermögen nach (17) direkt aus den Kanalzahlen ((Max)) ermittelt werden. Zur Fehlerabschätzung sind anhand der Streuung der Punkte insbesondere Fehlergrenzen für
zu berücksichtigen.
Zu Aufgabe 5 (Absorptionskoeffizient)
Die Bestimmung des Absorptionskoeffizienten bzw. der Halbwertsdicke wird mit der 0,662-MeV-Linie von 137Cs durchgeführt. Es sind verschiedene Bleiabsorber vorhanden, die zwischen Quelle und Detektor gebracht werden können. Intensitätswerte (Impulse pro Zeit) können mit der Funktion Fläche (Menü Messung) bestimmt werden, bei der die Impulszahl und die Impulsrate zwischen zwei Kanälen als Grenzen ausgegeben werden.
Für einwandfreie Ergebnisse muss der "Untergrund" durch natürliche Strahlung berücksichtigt werden. Überlegen Sie den Beitrag des Untergrundes und eine Methode der quantitativen Berücksichtigung. Die Berechnung des Absorptionskoeffizienten bzw. der Halbwertsdicken geschieht nach (15) und (16) durch eine logarithmische Darstellung der Intensitäten gegen die Absorberdicken.
Literaturwerte
Halbwertsdicke für -Strahlung (Kohlrausch; Praktische Physik 3; Teubner Stuttgart), dort ohne Fehlerangabe: