DokuWiki

<texit info> author=MySelf title=MyTitle </texit>

XXX

Messung der Schallgeschwindigkeit in Luft durch Laufzeitmessung.

Beobachtung der Resonanzen einer Luftsäule mit abgeschlossenem bzw. offenem Ende durch Variation der Anregungsfrequenz. Berechnung der Schallgeschwindigkeit und des Verhältnisses der spezifischen Wärmen c_p/c_V = <m>kappa</m> von Luft (Isentropenindex, Adiabatenkoeffizient).

Bestimmung der Schallgeschwindigkeit in Metallen aus der Laufzeit bzw. der Grundschwingungsfrequenz für zwei verschiedene Einspannungen der Stäbe (Messing und Stahl). Berechnung des Elastizitätsmoduls der Metalle.

(Zur Vorbereitung als Teil des Berichts): Kurze Darstellung der Schallausbreitung in Gasen. Berechnung der Temperaturabhängigkeit der Schallgeschwindigkeit. Diskussion stehender Wellen und Resonanzen in begrenzten Medien bei unterschiedlichen Randbedingungen (Luftsäulen, unterschiedlich eingespannte Stäbe).

In ausgedehnten, elastischen Medien führt eine zunächst lokale Erregung ("Störung", Auslenkung aus der Ruhelage, Druckschwankung) über die elastischen Kräfte zu einer Beeinflussung benachbarter Volumenelemente. So entsteht aus der Anregung eine Welle, die sich räumlich ausbreitet (Schallwelle). Die Ausbreitungsgeschwindigkeit c (Phasen­geschwindigkeit, Schallgeschwindigkeit) wird dabei bestimmt durch die Rückstellkräfte (Rückstellkonstante D) und durch die Trägheit der zu beschleunigenden Masse (Dichte <m>rho</m>).

<m> (1) c=sqrt{D/rho} </m>

In einem Festkörper, wo jedes Volumenelement eine definierte Ruhelage besitzt, können sich longitudinale Dichtewellen oder transversale Scherwellen ausbilden, wobei die Rück­stellkonstanten durch den Elastizitätsmodul E bzw. den Schermodul G gegeben sind. In Gasen und Flüssigkeiten gibt es nur Dichtewellen (Druckwellen), und die Rückstell­konstante ist gleich dem Kompressionsmodul K. Bei Gasen findet wegen den vergleichsweise kurzen Periodendauern von Schall­schwingungen und der schlechten Wärmeleitfähigkeit praktisch kein Energieaustausch zwischen den einzelnen Volumenelementen statt, so daß für die Zustandsänderungen die Adiabatengleichungen (Poisson-Gleichungen) gelten. Aus der Poisson-Gleichung p(V;<m>kappa</m>) folgt durch Ableiten für den Kompressionsmodul K:

<m> (2) pV^{kappa} = const </m>

und

<m> (3) K = V dp/dV = - kappa rho </m> wobei <m>kappa</m> das Verhältnis der spezifischen Wärmen cp/cV ist (Isentropenindex oder Adiabatenkoeffizient). Als Schallgeschwindigkeit erhält man damit:

<m> (4) c = sqrt{kappa p/rho} = c(T) </m> Die Schallgeschwindigkeit ist unabhängig vom Druck, da Trägheits- und Rückstellgröße (Dichte und Kompressibilität) in gleicher Weise vom Druck abhängen. Sie ist aber temperaturabhängig wegen der zusätzlichen Temperaturabhängigkeit der Dichte.

In einem begrenzten Volumen tritt durch Reflexion und Interferenz eine Folge (Ordnungs­zahl n) stationärer Schwingungszustände auf (stehende Wellen), wenn die Wellenlänge <m> lambda </m> in einem bestimmten Verhältnis zur Resonatorlänge l steht. Für einen einseitig abgeschlossenen Resonator gilt:

<m> (5a) l = (n - 1/2) lambda/2 </m>

Für einen beidseitig abgeschlossenen Resonator:

<m> (5b) l = n lambda/2 </m>

Bei bekannter Wellenlänge und Frequenz kann die Schallgeschwindigkeit dann mit der Fundamentalbeziehung für Wellen berechnet werden:

<m> (6) c = lambda nu </m>

Die Resonanzen stellen die möglichen Anregungszustände des Systems dar, in die hinein auch bei einer impulsförmigen Anregung die Anregungsenergie übertragen wird. Eine Stoßanregung wird zunächst als Stoßwelle in dem Resonator hin- und herlaufen. Im Bild der Fourierzerlegung besteht sie jedoch aus einem ganzen Spektrum von Anregungs­frequenzen, wobei die unpassenden Frequenzen und die resonanten Oberschwingungen wegen der höheren Auslenkungsgeschwindigkeiten stärker gedämpft werden, so daß nach genügend langer Zeit allein die sinusförmige Grundschwingung übrig bleibt. Zu Aufgabe 2 können durch Wahl des Beobachtungszeitpunktes (Zeitfenster) das unterschiedliche Verhalten untersucht und beide Grenzfälle (Pulsausbreitung, Schwingungszustand) beobachtet werden. Kurz nach der Stoßanregung treten scharfe Impulse auf, deren Laufzeit gemessen werden kann. Einige Zeit nach der Anregung (hier: einige Sekunden) kann dann die sich ausbildende Grundschwingung beobachtet werden.

Zwei Mikrofone; Schallerzeuger (Patsche). Metallmaßstab. Resonanzrohr fester Länge mit Lautsprecher und Mikrofon. Funktionsgenerator mit Zähler. Multimeter zur Messung des Mikrofon-Ausgangssignals. Metallstab mit zwei Einspannvorrichtungen. COMEX-Transientenrekorder (siehe dazu Skripte COMEX und TRANSIENTEN­REKORDER im allgemeinen Teil der Praktikumsanleitung).

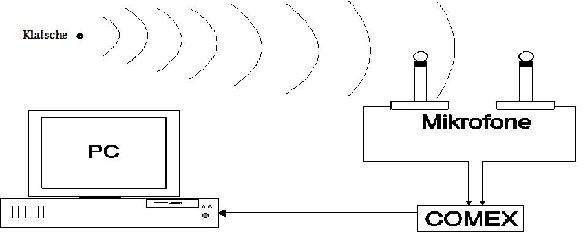
Abb. 1: Skizze des Versuchsaufbause der Laufzeitmessung.

Zwei Mikrofone werden in definiertem Abstand aufgestellt, und die Ausgangssignale eines Schallimpulses (Knall) mit einem Zweikanal-Transientenrekorder parallel aufgenommen. Der gemessene Zeitunterschied ist dann gleich dem Laufzeitunterschied des Schallsignals von der Quelle. Bei den Messungen ist auf eine „richtige Geometrie“ des Aufbaus zu achten. Variieren Sie den Abstand der Mikrofone.

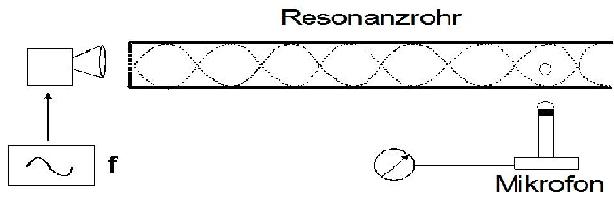
Abb. 2: Skizze des Versuchsaufbause der Resonanzmessung einer Luftsäule.

Mit einem Funktionsgenerator und einem Lautsprecher werden in dem Resonanzrohr (mit und ohne Abschlußdeckel) stehende Schallwellen angeregt und mit einem Mikrofon nachgewiesen. Die Mikrofon-Ausgangsspannung kann mit einem Multimeter gemessen werden. Gemessen werden die Resonanzfrequenzen in Abhängigkeit von der Ordnungszahl. Zur Auswertung gemäß (5a,b) soll ein numerisches Auswerteverfahren entwickelt werden, um der hohen Genauigkeit der Messungen zu entsprechen. Bei der Diskussion der Ergebnisse ist zu entscheiden, ob das durch den Lautsprecher begrenzte Ende des Rohres als offenes oder als geschlossenes Ende zu betrachten ist. Zur Berechnung der Schallgeschwindigkeit nach (3) muß die Temperaturabhängigkeit berücksichtigt werden, wobei Luft in guter Näherung als ideales Gas betrachtet werden kann. Die Temperatur kann im Versuchsraum gemessen werden.

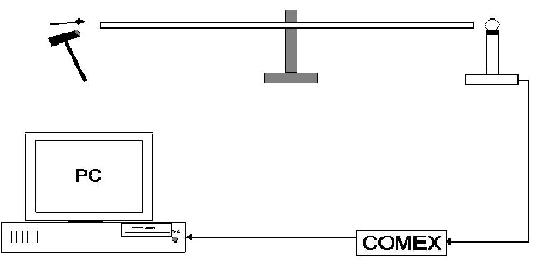
Abb. 3: Skizze des Versuchsaufbause zur Bestimmung der Schallgeschwindigkeit in Metallen.

Die Experimente und Messungen werden zunächst an dem mittig eingespannten Stab durchgeführt. Mit einem sehr dicht vor die Stirnseite des Stabes gestellten Mikrofon kann die Auslenkung des Stabendes nach Anregung durch Anschlagen mit einem kleinen Hammer registriert werden. Beobachten Sie die zeitliche Veränderung der Schwingungs­formen durch Start der Messung (Transientenrekorder) zu verschiedenen Zeiten. Wie verändern sich die Schwingungsformen nach dem Anschlagen? Wann tritt die Grund­schwingung deutlich hervor? Drucken Sie charakteristische Diagramme für die Grenzfälle aus. Beobachten und diskutieren Sie die Schwingungsbilder auch für eine (sinnvolle) zweifache Einspannung des Stabes. Die Dichte des Stabes muß gemessen werden (Waage und Schiebelehre in Raum 2.05).

Warum werden höhere Frequenzen stärker gedämpft als niedrigere?