Table of Contents
<texit info> author=steinbrügge title=v10 Radioaktivität </texit>
V10 - Versuchsanleitung
<texit info> author=steinbrügge title=V10 Radioaktivität </texit>
| V10 | RADIOAKTIVITÄT |
|---|
Einleitung
Unter Radioaktivität versteht man den spontanen Zerfall radioaktiver Atomkerne. Dabei werden oder
-Strahlen, deren Einwirkung auf lebendes Gewebe verschieden starke Schäden zur Folge hat, ausgesandt. Diese beruhen auf der Inaktivierung von Enzymen, der Auslösung von Mutationen, der Bildung von Ionen und vor allem von freien Radikalen. In der Medizin finden radioaktive Nuklide bei der Diagnostik und der Therapie Verwendung. Die nuklearmedizinische Diagnostik verwendet in der Regel die
-Strahlung und zwar in vivo zur Lokalisationsdiagnostik durch Szintigraphie (z.B. zur Tumorlokalisation) und zur Funktionsdiagnostik (z.B. der Nieren, der Lungen, und der Schilddrüse) und in vitro zur Labordiagnostik (z.B. zur Markierung von Hormonen mit radioaktiven Nukliden (Insulinbestimmung)).
In der nuklearmedizinischen Therapie werden radioaktive Nuklide hauptsächlich zur Bestrahlung von Geschwulsterkrankungen von außen oder durch Implantate eingesetzt. Eine gezielte Bestrahlung einzelner Organe kann durch die Lokalisierung der Wirkung über Implantation im betreffenden Organ oder durch Anreicherung radioaktiv markierter Stoffe im betreffenden Organ über den natürlichen Stoffwechselvorgang erreicht werden. In beiden Fällen werden die gewünschten hohen lokalen Bestrahlungsdichten erreicht.
Ungenügende Kenntnis über den Strahlenschutz bringt Gefahren für den Patienten und den behandelnden Arzt. Daher unterliegt die Anwendung solcher Verfahren strengen gesetzlichen Bestimmungen.
Drei Grundregeln (AAA-Regeln) sind beim Arbeiten mit radioaktiven Strahlungsquellen von höchster Wichtigkeit:
- Abschirmen der radioaktiven Quelle (z.B. durch einen Bleimantel)!
- Aufenthaltsdauer in der Nähe radioaktiver Quellen möglichst kurz halten!
- Abstand zu radioaktiven Quellen möglichst groß halten!
Das Abstandsgesetz und das Absorptionsgesetz, auf deren Anwendung die dritte und die erste der drei AAA-Regeln beruhen, bilden den Schwerpunkt der vorliegenden Versuchsbeschreibung.
Aufgabenstellung
- Bestimmen Sie den Nulleffekt.
- Überprüfen Sie das Abstandsgesetz.
- Überprüfen Sie das Absorptionsgesetz und bestimmen Sie die Halbwertsdicke der Absorptionsmaterialien Aluminium, Blei, Kupfer und Plexiglas.
- Bestimmen Sie die Aktivität der radioaktiven Quelle.
Erläuterungen zur Versuchsdurchführung
Im Versuch wird ein -Strahler als radioaktive Quelle benutzt. Während einer vorgewählten Zeit T wird die auf ein Geiger-Müller-Zählrohr treffende Strahlung in Form von Impulsen N gemessen und von einem Zählwerk angezeigt. Bei allen Versuchen wird die Messzeit T = 120s gewählt, um noch einen Wert N mit tolerierbarem statistischem Fehler ΔN zu erreichen. Als radioaktives Präparat verwenden wir eine sehr geringe Menge des künstlich hergestellten Kobalt Isotops 60Co, das sich unter Aussendung von
und
-Strahlung in das stabile Nickel-Isotop 60Ni umwandelt (siehe Abschnitt 10.4.2). Die relativ energiearme
-Strahlung kann die Wände des Probengefäßes nicht durchdringen, so dass nur die
-Strahlung gemessen wird. Die radioaktive Quelle und das Zählrohr sind auf einer Schiene verschiebbar angeordnet, wobei der Abstand R an einem Maßstab ablesbar ist. Zwischen Quelle und Empfänger kann ein Halter zur Aufnahme von Absorptionsplatten (Gesamtdicke d) aufgestellt werden (siehe Abbildung 10.1).
BILD 10_1 EINFÜGEN
Das Messprinzip mit einem Geiger-Müller-Zählrohr wird in Abschnitt 10.4.1 erläutert. An dieser Stelle soll nur die Bedienung des Geräts zur Versuchsdurchführung kurz beschrieben werden:
- Einschalten des Gerätes: Taste ON/OFF.
- Gerät ein paar Minuten warmlaufen lassen.
- Vor jeder Messung wird das Zählwerk mit der Taste RESET und die Stoppuhr durch Drücken der weißen Taste auf Null gesetzt.
- Zu Beginn jeder Messung drücken Sie gleichzeitig die Taste START des Zählwerks und die grüne Taste der Stoppuhr.
- Nach T = 120s drücken Sie gleichzeitig die Taste STOP des Zählwerks und die rote Taste der Stoppuhr.
- Lesen Sie die zugehörige Impulszahl N ab und notieren Sie sie in Ihrem Protokollheft.
Messungen und Auswertungen
Der Nulleffekt
Statistische Schwankungen bei Zählungen
Der Zerfall radioaktiver Substanzen unterliegt statistischen Schwankungen. Zählt man bei konstanter mittlerer Strahlungsintensität während einer bestimmten Zeit T die Zählrohrimpulse, so erhält man bei n-facher Wiederholung der Messung die um einen Mittelwert N schwankenden Ergebnisse N1,N2,…,Nn. Als Maß für die Schwankungen benutzt man die Standardabweichung ΔN (auch mittlerer quadratischer Fehler der Einzelmessung genannt). Die Anwendung der Statistik auf solche Prozesse ergibt die einfache Formel
(10.1)
Der relative Fehler ΔN/N der Zählungen wird also umso kleiner, je mehr Impulse gezählt werden, d.h. je größer die Messzeit T gewählt wird.
Der Nulleffekt N0
Auch wenn man alle radioaktiven Quellen aus der Umgebung des Zählrohrs entfernt, zählt dieses dennoch eine gewisse (geringe) Zahl N0 von Impulsen. Sie wird durch die kosmische Strahlung (Höhenstrahlung) sowie durch Spuren radioaktiver Substanzen im Zählrohrmaterial verursacht. Dieser Nulleffekt wird gemessen, bevor das radioaktive Präparat an seinen Platz gebracht wird. N0 wird bei allen nachfolgenden Messungen von der Gesamtimpulszahl Nges abgezogen (siehe auch Abschnitt 10.3.2)!
Um N0 trotz der kurzen Messzeit von T = 120s mit einiger Sicherheit zu bestimmen, wird die Messung mehrmals wiederholt und gemittelt (siehe tabelle 10.1).
Tabelle 10.1 Beispiel zur Bestimmung von 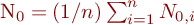 und
und
 aus drei (n = 3) Einzelmessungen N0,1, N0,2, N0,3 .
aus drei (n = 3) Einzelmessungen N0,1, N0,2, N0,3 .
| Messung i | 1 | 2 | 3 |
| N0,i | 32 | 38 | 34 |
| N0=(32+38+34)/3 ΔN0 = |
|||
Das Abstandsgesetz
Die radioaktive Strahlung wird von der Quelle in alle Richtungen ausgesandt und breitet sich geradlinig aus. Außerdem gestattet es die Versuchsanordnung, die Quelle als punktfö}rmig zu betrachten. Unter dieser Voraussetzung nimmt die vom Präparat herrührende Impulszahl NP mit dem Quadrat des oben eingeführten Abstands ab:
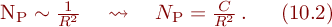
Das Abstandsgesetz gilt natürlich nur für die vom radioaktiven Präparat verursachte Impulszahl NP, während die oben erläuterte Impulszahl N0 (Nulleffekt) unabhängig von R ist. Wir messen als Gesamtimpulszahl Nges aber stets die Summe beider Teilimpulszahlen.NP muss also durch Differenzbildung von Nges mit N0 ermittelt werden:
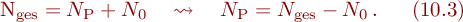
Die Überprüfung des Abstandsgesetzes sei hier am Beispiel von acht Einzelmessungen gezeigt. Gemessen wird jeweils die Impulszahl Nges = Nges(R). Dabei wird R sinnvoll jeweils um einen Faktor 1.2 bis 1.3 verändert (warum tut man dies nicht in äquidistanten Schritten?). Der gemittelte Wert für den Nulleffekt N0 und ΔN0 werden in diesem Beispiel aus den in Tabelle 10.1 aufgeführten Messungen übernommen. Die Messergebnisse NP(R)d\beta\gamma, \ldots$ </latex> |
| Isotope | Atomkerne mit gleicher Ordnungszahl z, aber verschiedener Neutronenzahl n (Beispiel: die Sauerstoffisotope 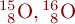 und und 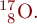 Isotope sind chemisch im Wesentlichen äquivalent. Nur Prozesse, die von der Masse abhängen, zeigen für Isotope ein leicht unterschiedliches Verhalten (Unterschiede in den physikalisch-chemischen Gleichgewichten, Unterschiede in der Diffusionsgeschwindigkeit, Isotopieverschiebungen in den Atomspektren,…). Diese Erscheinungen werden als Isotopieeffekte bezeichnet. Isotope sind chemisch im Wesentlichen äquivalent. Nur Prozesse, die von der Masse abhängen, zeigen für Isotope ein leicht unterschiedliches Verhalten (Unterschiede in den physikalisch-chemischen Gleichgewichten, Unterschiede in der Diffusionsgeschwindigkeit, Isotopieverschiebungen in den Atomspektren,…). Diese Erscheinungen werden als Isotopieeffekte bezeichnet. |
| α-Strahlung | Emission von Helium-Kernen der Massenzahl a=4 und der Kernladungszahl z=2:  . Typische Energien der α-Teilchen liegen zwischen 4MeV und 9MeV. . Typische Energien der α-Teilchen liegen zwischen 4MeV und 9MeV. |
| β-Strahlung | β-Strahlung besteht aus schnell fliegenden Teilchen kleiner Masse (Positronen, Elektronen), die in elektrischen oder magnetischen Feldern stärker als α-Strahlen abgelenkt werden. |
| γ-Strahlung | Kurzwellige elektromagnetische Strahlung (noch kurzwelliger als die Röntgenstrahlung). γ-Strahlung wird in elektrischen oder magnetischen Feldern nicht abgelenkt. |
| Aktivität | Maß für die Zerfallsrate eines Radionuklids. Sie berücksichtigt nicht die biologische Wirksamkeit der Strahlungsarten. Die Aktivität A gibt die Anzahl der Zerfälle N pro Zeit t an:  . Die SI-Einheit der Aktivität ist [A]=1Bq (Becquerel) = 1 Zerfall pro Sekunde. Die früher benutzte Einheit von 1Ci (Curie) ist historisch entstanden und entspricht der Anzahl der Zerfälle von 1g . Die SI-Einheit der Aktivität ist [A]=1Bq (Becquerel) = 1 Zerfall pro Sekunde. Die früher benutzte Einheit von 1Ci (Curie) ist historisch entstanden und entspricht der Anzahl der Zerfälle von 1g 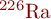 pro Sekunde: pro Sekunde: 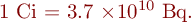 |
| Ionendosis Dq | 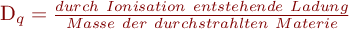 ; [D_q]= 1C/kg = 1A.s/kg; 1R (Röntgen) = 2.58 x 10-4 C/kg. ; [D_q]= 1C/kg = 1A.s/kg; 1R (Röntgen) = 2.58 x 10-4 C/kg. |
| Energiedosis DE | 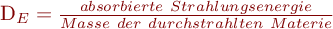 ; [DE] = 1Gy (Gray) = 1J/kg; bis 1985 wurde das rad verwendet: ; [DE] = 1Gy (Gray) = 1J/kg; bis 1985 wurde das rad verwendet: 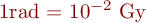 . Energiedosis und Ionendosis lassen sich ineinander umrechnen, da die aus der Strahlung absorbierte Energie proportional zur dadurch entstandenen Ladung ist. Für Luft gilt beispielsweise: 1R = 0.87rad. . Energiedosis und Ionendosis lassen sich ineinander umrechnen, da die aus der Strahlung absorbierte Energie proportional zur dadurch entstandenen Ladung ist. Für Luft gilt beispielsweise: 1R = 0.87rad. |
| Biologische Dosis | Die pro Zeit aufgenommene Ionen- bzw.\ Energiedosis. |
| biologische Schädlichkeit | Die biologische Schädlichkeit hängt nicht nur von der Menge der absorbierten Energie bzw.\ der Menge der entstandenen Ionen (also von DE und Dq) ab, sondern auch von der Strahlenart. Bei gleicher Energie sind α-Strahlen wesentlich gefährlicher als β-Strahlen und γ-Strahlen. Zur Berücksichtigung der biologischen Schädlichkeit wird der Bewertungsfaktor Q eingeführt. Er beträgt für β- und γ-Strahlung 1, für α-Strahlung nimmt Q Werte zwischen 10 und 20 an. |
| Äquivalentdosis | Berücksichtigung der unterschiedlichen Wirksamkeit von verschiedenen Strahlungsarten: H = Q.DE Die Einheit der Äquivalentdosis ist gleich der Einheit der Energiedosis (da Q dimensionslos ist). Zum Unterscheiden der beiden Größen wurde aber eine weitere Einheit eingeführt: [H] = 1Sv (Sievert) = 1J/kg. Bis 1979 diente das rem als Einheit für die Äquivalentdosis: 1rem = 10-2 Sv. 1rad entspricht 1rem für β- und γ-Strahlen. 1rad entspricht 10 bis 20rem für α-Strahlen. |
